Косвенные показатели качества
Рассмотрим, как влияет на переходной процесс расположение корней характеристического уравнения на комплексной плоскости на примере системы, описываемой дифференциальным уравнением третьего порядка.
Характеристическое уравнение имеет три корня и соответствующее решение выглядит так:
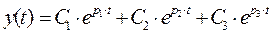 .
.
Будем иметь ввиду устойчивую систему, то есть все корни имеют отрицательную действительную часть.
Для действительных корней кривая у (t) переходного процессамонотонная, рис. 6.3.
Если два корня комплексных и один действительный, причем действительный расположен ближе к мнимой оси, а комплексные дальше, то кривая переходного процессаприобретает слабо выраженную колебательность, рис. 6.4.
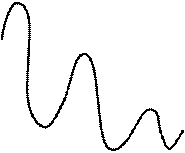
Если комплексные корни располагаются вблизи мнимой оси, а действительный дальше, переходной процесс приобретает ярко выраженный колебательный характер, рис.6.5. Чем ближе комплексные корни к мнимой оси, тем медленнее затухают колебания, тем длительнее переходной процесс (больше время tp). Чисто мнимые корни дают незатухающие гармонические колебания.
Найдем условие, при котором регулируемая величина у (t) станет меньше в m раз за время регулирования. То есть, у (t) уменьшится до величины порога нечувствительности Δ.

Рис. 6.3. Монотонная кривая переходного процесса.

|
 V y (t)
V y (t)
 | |||||
 | |||||
 | |||||

 0 t
0 t
6.4. Апериодический процесс с колебательной составляющей.

|
 V y (t)
V y (t)
 | |||||
 | |||||
 | |||||
 |
 0 t
0 t
Рис. 6.5. Затухающий колебательный процесс.
Для заданного времени tp требуется, чтобы корни рi имели отрицательную действительную часть s менее некоторой отрицательной величины a, рис. 6.6.

 V y (t)
V y (t)

 y (0) = C
y (0) = C
 |
|
|


 М
М


|




 a
a
Рис. 6.6. Рис. 6.7.
Пусть время регулирования tp обеспечивается корнем çs ê= a. Влиянием остальных корней пренебрегаем. Соответствующая этому корню кривая переходного процесса представлена на рис. 6.7. Она имеет уравнение
y (t) = Ce- at.
В начальный момент y (0) = C. В момент времени tp кривая пересечет порог нечувствительности. В точке М, где кривая пересекается с прямой y = D
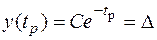 .
.
Величина y (tp) станет меньше в m раз по сравнению с величиной в начальный момент. То есть,
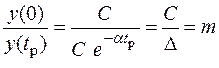 .
.
То есть,
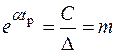 .
.
Логарифмируя, получаем:

Значит, величина действительной части корня, обеспечивающего заданное время регулирования, должна быть:
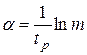 . (6.6)
. (6.6)
Формула (6.6.) дает приближенную оценку a, потому что остались без внимания другие слагаемые полного решения уравнения.
Параметр a называют «запас устойчивости» или «степень устойчивости». Это абсолютное значение действительной части ближайшего к мнимой оси корня.Чем меньше a, тем ближе система к границе устойчивости, тем больше время регулирования. При a = 0 (система на границе устойчивости) время регулирования становится бесконечно большим.
Рассмотрим еще одну характеристику распределения корней: угол q между отрицательной полуосью абсцисс и прямой, проведенной из начала координат к корню с максимальной мнимой частью, рис. 6.8. В этот угол вписывается половина всех наиболее удаленных от мнимой оси корней. Корень с максимальной мнимой частью дает наибольший вклад в колебания. Величину
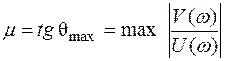 (6.7)
(6.7)
называют колебательностью системы или коэффициентом затухания системы. Чем меньше угол q, тем меньше колебательность.

 V
V
 | |||
 | |||



 0 U
0 U
 |
Рис. 6.8.
Найти время регулирования для трех характеристических уравнений:
2 p 2 + p + 1 = 0,
p 2 +2 p + 1 = 0,
p 2 + p + 2 = 0.
Требуется, чтобы управляемая величина уменьшилась за время регулирования в е раз. (е = 2,718).
1. Корни уравнения 2 p 2 + p + 1 = 0 будут:
p 1 = -0,25 + j 0,66, p 2 = -0,25 – j 0,66.
т.е. a = 0,25. 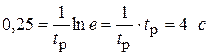 .
.
2. Корни уравнения p 2 +2 p + 1 = 0 будут:
p 1 = -1, p 2 = -1.
т.е. a = 1, tp = 1 c.
3. Корни уравнения p 2 + p + 2 = 0 будут:
p 1 = -0,5 + j 1,32, p 2 = -0,5 – j 1,32
т.е. a = 0,5, tp = 2 c.
Для переходной функции инерционного звена:
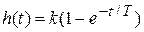
найти, через какое время t * величина h (t) будет отличаться от своего предельного значения на e единиц?
Предельное значение – это k единиц (при t = ∞)
Решение должно подчиняться условию h = k - e при t = t * Введем его в переходную функцию
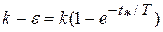
и получим: e = kexp(- t */ T). Посредством логарифмирования находим:
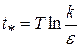 .
.
 2014-02-02
2014-02-02 493
493








