Прямые показатели качества. 1. Попов Е.П. Теория линейных систем автоматического регулирования и управления

Литература

1. Попов Е.П. Теория линейных систем автоматического регулирования и управления. – М.: Наука, 1989. – 304 с.

2. Егоров К.В. Основы теории автоматического регулирования. – М.: Энергия, 1967. – 648 с.

3. Востриков А.С., Французова Г.А. Теория автоматического регулирования. – М.: Высшая школа, 2004. – 365 с.

4. Бесекерский В.А., Попов Е.П. Теория автоматического регулирования. – М.: Наука, 1974 – 992с.

1. Иващенко Н.Н. Автоматическое регулирование. Теория и элементы систем. – М.: Машиностроение, 1973. – 606 с.

2. Фельдбаум А.А., Бутковский А.Г. Методы теории автоматического управления. – М.: Наука, 1971. – 744 с.

3. Теория автоматического управления. Часть 1./ Под ред. А.В. Нетушила. – М.: Высшая школа, 1968. – 424 с.

Помимо требования быть устойчивой, к системе автоматического регулирования предъявляется требование по качеству регулирования. Необходимо, чтобы САР удовлетворяла ряду требований, связанных с переходным режимом и установившимся режимом.

Качество переходного процесса определяется совокупностью показателей, характеризующих приближение реального процесса к желаемому. О показателях судят, измеряя ряд величин в переходном процессе при единичном ступенчатом воздействии.

Показатели качества в переходном режиме подразделяют на прямые и косвенные. Прямые получают непосредственно по переходной функции. Косвенные рассчитывают.

Основной характеристикой качества САР является точность, которая оценивается ошибкой регулирования

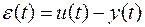. (6.1)

Пример появления ошибки регулирования в системе автоматической стабилизации показан схемой на рис. 6.1. Система должна обеспечивать равенство управляемой величины y (t) задающему воздействию u (t) при действии возмущения z (t). Регулятор обозначен передаточной функцией W ₁(p), объект управления – передаточной функцией W ₂(p).

z (t)

u (t) e (t) x (t) y (t)

W ₁ W ₂

Рис. 6.1. Замкнутая система

автоматического регулирования.

Нетрудно убедиться, что ошибка регулирования зависит от задающего воздействия и от возмущения. Для этого, методом обратного движения построим операторное уравнение

.

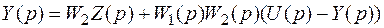Запишем уравнение по Лапласу ошибки

E (p) = U (p) – Y (p),

учтем формулу передаточной функции по ошибке

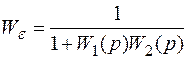
и после простых алгебраических действий получим:

.

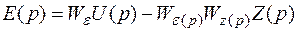Первое слагаемое делает вклад в ошибку регулирования от задающего воздействия, второе – от возмущения. Передаточные функции представляют свойства системы.

Введем в формулу (6.1) условие единичного ступенчатого воздействия, u (t) = 1(t). Тогда переходной функцией будет h (t). Ошибка получает вид

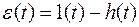. (6.2)

Формула (6.2) показывает, что ошибка отличается от переходной функции на постоянную величину. Поэтому, оценивая качество, в формулах можно использовать непосредственно переходную функцию. При импульсном воздействии ошибка регулирования будет отличаться от таковой при единичном ступенчатом воздействии.

С течением времени h (t) стремится к установившемуся значению h (∞), а ошибка регулирования – к некоторому постоянному значению

.

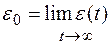Это значение ошибки называют статической ошибкой. Статическая ошибка есть рассогласование между установившемся значением регулируемой величины и ее заданным значением:

.

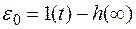Смысл статической ошибки заключается в следующем. Система исполняет регулирующую команду не до конца: когда достигается установившееся состояние, остается некоторое остаточное отклонение регулируемого параметра от заданного значения. Остаточное отклонение зависит от конструктивных особенностей САР и от величины управляющего воздействия.

Разность

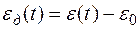(6.3)

называют динамической ошибкой.

Систему автоматического регулирования с остаточной ошибкой в установившемся режиме называют статической системой.

Наряду со статическими, есть системы, у которых регулируемый параметр по достижении равновесия принимает точно заданное значение. Систему автоматического регулирования, которая исполняет регулирующую команду точно, называют астатической.

Подводя итог сказанному, можно констатировать:

- показатель качества «точность» оценивается двумя ошибками: статической и динамической;

- регулирование статической системы происходит с ошибкой.

- астатическая система регулируется без ошибки.

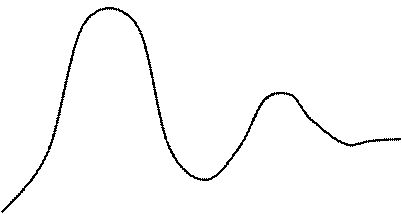
Быстродействие. Оценивается временем регулирования t_p, рис. 6.2. Это промежуток времени, по истечении которого отклонение выходной величины от установившегося значения h (¥) не превышает некоторой заранее заданной величины Δ. Последняя носит название «поры нечувствительности».Обычно назначают Δ в пределах (0,01 … 0,05) h (∞).

h (t)

h _max

2 Δ

h (∞)

0 t _н t _м t _p

Рис. 6.2. Переходная функция

Наряду с t_p для колебательных процессов используют две другие оценки быстродействия. Одна из них – время t _н от начала процесса до первого пересечения кривой h (t) с прямой h = у (¥), рис. 6.2. Время t _н называют временем нарастания переходного процесса. Другая – время t _м достижения первого максимума, рис. 6.2.

Перерегулирование. Это максимальное отклонение регулируемой величины от установившегося значения h (¥). Определяется в процентах:

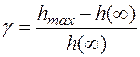(6.4)

h_max – величина h (t) в момент времени t_м, рис. 6.2.

Чем больше g, тем более система склонна к колебаниям.

Число колебаний регулируемой параметра h (t) за время регулирования t_p. Период колебаний определяется как 2p/ w. Частное от деления времени регулирования на период колебаний есть число колебаний

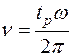. (6.4)

Число колебаний регулируемой величины оценивает показатель переходного процесса, называемый «колебательность». Высокая колебательность отвечает большой амплитуде или частоте колебаний, медленному затуханию. В этом случае величина ν тоже большая. Низкой колебательности отвечает малая величина ν.

Специфические особенности системы регулирования могут потребовать дополнительные оценки качества. Например, точность воспроизведения входного сигнала, величина ошибки от возмущения и др.