Конспект лекций 1 страница. Глава 10. Явление электромагнитной индукции

Глава 10. Явление электромагнитной индукции

Глава 9. Магнитное поле тока

Глава 8. Постоянный электрический ток.

Глава 7. Электростатика

Глава 6. Термодинамика.

Глава 5. Кинетическая теория

Глава 4. Динамика вращательного движения.

Глава 3.Законы сохранения в механике.

Глава 2. Динамика материальной точки.

Глава 1. Кинематика.

§1.1. Система отсчета. Инерциальные системы отсчета. Принцип относительности.

Всякое движение есть изменение состояния физического объекта. Фундаментальным свойством природы является относительность движения. Механическим движением называется перемещение тел или частей тела друг относительно друга. Для его описания необходимо выбрать тело отсчета. Во многих технических задачах механики это земля или неподвижные относительно земли тела. Движение происходит в пространстве и во времени, их совокупность (способ отсчета времени – «часы» и тело отсчета) образует систему отсчета, с которой связывают систему координат. Из опыта следует, что пространство трехмерно и подчиняется геометрии Эвклида на расстояниях, малых по сравнению с размерами Вселенной, и что для нерелятивистских движений (v << c) время для всех тел течет одинаково. В таком случае систему отсчета изображают декартовой системой координат. Пространство и время всегда рассматриваются в конкретной системе отсчета, поэтому пространство и время относительны, как относительно движение.

Системы отсчета можно связывать с разными телами. В системе отсчета, связанной с землей, станционные строения покоятся, а в системе отсчета, связанной с движущимся поездом, они могут двигаться с разными скоростями и ускорениями. Преимуществом в физике пользуются инерциальные системы отсчета, связанные со свободными телами. Свободным называется тело, настолько удаленное от всех прочих тел, что их воздействием на движение данного тела можно пренебречь. В инерциальной системе отсчета справедлив принцип инерции Галилея, он же первый закон Ньютона: в инерциальной системе отсчета свободное тело покоится или движется равномерно и прямолинейно. Следовательно, любая система отсчета, покоящаяся или движущаяся равномерно и прямолинейно относительно инерциальной, также является инерциальной. Опыт показывает, что инерциальной является система, связанная со звездами, в частности, гелиоцентрическая. Она образована Солнцем как телом отсчета совместно с неподвижными относительно него часами. Три взаимно перпендикулярные оси пересекаются в центре Солнца и ориентированны по трем одиночным звездам. На практике чаще всего рассматриваются движения тел относительно земли, и тогда систему отсчета удобно связывать с землей. Такая система называется геоцентрической. Однако эта система неинерциальна в силу двух причин: центр Земли движется вокруг Солнца, и Земля вращается вокруг собственной оси. Доказательством неинерциальности Земли является маятник Фуко. Он представляет собой массивный груз, подвешенный на длинной проволоке. Например, маятник Фуко в Исаакиевском соборе в Ленинграде, имел длину 98 м. Плоскость качания маятника относительно звезд сохраняет свою ориентацию. Вследствие суточного вращения Земли наблюдатель, находящийся на Земле и вращающийся вместе с ней, видит, как плоскость качания маятника медленно поворачивается относительно земной поверхности в сторону, противоположную вращению Земли. Центростремительное ускорение Земли при ее вращении вокруг Солнца составляет около 6^.10^-3 м/с², центростремительное ускорение при суточном вращении Земли около 3^.10^-2 м/с². В задачах, где требуемая точность позволяет пренебречь этими численными значениями по сравнению с численным значением ускорения свободного падения g = 9,8 м/с², Землю можно считать инерциальной системой отсчета.

Преимущественное использование инерциальных систем отсчета по сравнению с неинерциальными системами отсчета связано с универсальным законом природы - принципом относительности. Он гласит: все законы физики имеют одинаковый вид во всех инерциальных системах отсчета. Другими словами, никакими опытами, проводимыми внутри инерциальной системы отсчета, нельзя определить, покоится она или движется равномерно и прямолинейно. Понятие абсолютного покоя лишено смысла.

Физические законы записываются в виде математических формул, имеющих одинаковый вид в любых инерциальных системах отсчета. Неизменность вида уравнений при каких-либо преобразованиях называется инвариантностью. Принцип относительности утверждает: физические законы инвариантны относительно перехода от одной инерциальной системы отсчета к другой. Именно принцип относительности обеспечивает воспроизводимость результатов опытов, проведенных при одинаковых условиях разными исследователями в разное время и в разных местах.

§1.2. Кинематика материальной точки.

1.Задача кинематики – описание механического движения. Кинематические характеристики – закон движения (в быту мы его обычно называем расписанием), скорость и ускорение. Знание одной из них как функции времени позволяет найти остальные две, и мы этим постоянно пользуемся в своей жизни.

2. Для теоретического описания физических объектов используют их модели. Простейшая модель механики – материальная точка. Материальной точкой или частицей называют тело, размеры которого, форма, внутренняя структура и протекающие в нем процессы в данной задаче не влияют на его движение. Например, рассматривая орбитальное движение Земли вокруг Солнца, ее можно считать материальной точкой. В других задачах, например, при изучении процессов, происходящих в земной коре (землетрясение), модель материальной точки неприемлема. Следует помнить о том, что в классической механике частицы должны быть классическими телами, а не квантовыми. Столь маленькие с обыденной точки зрения объекты, как электроны, создающие изображение на экране кинескопа, вполне соответствуют модели материальной точки, тогда как такие же электроны при своем движении в атоме являются квантовыми объектами, и модель материальной точки к ним не применима.

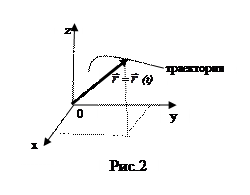3. Закон движения известен, если известно положение тела в пространстве в каждый момент времени. Этот закон может быть задан таблицей, графиком, уравнением (его называют кинематическим уравнением движения).

Положение материальной точки в пространстве указывает радиус - вектор , проведенный из начала отсчета в точку, где находится тело (рис. 2). При движении этот вектор изменяется со временем t, так что закон движения в векторной форме выражает уравнение:

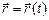(1.2.1)[1]

В декартовой системе координат этот же закон движения в координатной форме выражают три скалярных уравнения:

x=x(t)

y=y(t) (1.2.2)

z=z(t)

Согласие между законами движения в векторной (1.2.1) и в координатной (1.2.2) формах есть выражение принципа независимости движения: пространственное движение м.т. можно представить как сумму трех прямолинейных движений вдоль осей координат.

Линия, по которой движется тело, называется траекторией. Уравнение траектории задано законом движения. Закон движения в координатной форме (1.2.2) задает это уравнение в параметрической форме, где параметром является время t. Подчеркнем, что понятие траектории применимо только в классической физике, для квантовых частиц оно теряет смысл

Минимальное число параметров (координат), задающих положение тела, называется его числом степеней свободы – i. На рис 1 рассмотрено трехмерное движение м.т. (i = 3), движение по известной поверхности имеет две степени свободы и называется двухмерным, движение по известной траектории (например, поезда по рельсам или автомобиля по шоссе) называется одномерным. При одномерном движении закон движения превращается в одно скалярное уравнение:

s = s(t) (1.2.3)

В приведенном уравнении s – координата точки траектории. Если s= 0 – тело находится в начале отсчета, если s >0 или s <0 – тело смещено на расстояние s, измеренное вдоль траекторииот начала отсчета соответственно в положительном или в отрицательном направлениях.

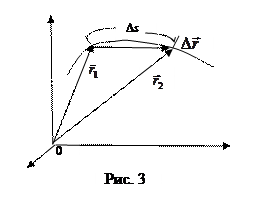
4. Следующая кинематическая характеристика движения – скорость – характеризует быстроту изменения положения тела в пространстве. Пусть положение тела в момент времени t₁ указывал радиус – вектор , а в момент времени t₂ радиус - вектор . Вектор перемещения (рис.3)

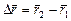(.1.2.4)

Путь Ds – расстояние, пройденное телом по траектории. При движении по прямолинейной траектории в одном направлении модуль вектора веремещения и пройденный путь равны друг другу: ½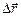½= Ds. Заметим, что по определению, путь – положительная арифметическая величина. Если направление движения тела изменяется на противоположное, то путь равен сумме длин, измеренных вдоль траектории, при любом направлении движения. Например, когда мы ушли из дома, а потом вернулись домой, то вектор перемещения равен нулю, а вот пройденный путь, и об этом свидетельствует наша усталость, совсем не равен нулю. В случае движения по криволинейной траектории, а также при изменении направления движения по траектории любой формы½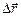½£ Ds.

Вектор средней скорости за промежуток времени D t = t₂ – t₁ равен:

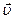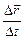
<>= (1.2.5)

Направление вектора средней скорости совпадает с направдением вектора перемещения. Из рис. 2 видно, что если рассматриваемый участок пути разделить на два одинаковых, то на каждом из них векторы средних скоростей будут различаться, так что <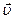> - довольно грубая характеристика движения. Для получения более точной характеристики надо рассматривать маленькие участки траектории, которым соответствуют маленькие промежутки времени. Предел выражения (1.2.5) при стремлении промежутка времени D t к нулю дает мгновенную скорость. В математике такую операцию называют нахождением производной, так что по определению вектор мгновенной скорости

(1.2.6)

Направлен 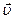по касательной к траектории, так что ему можно придать вид:

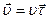(1.2.7)

где υ – модуль скорости, 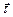- касательный орт, т.е. единичный вектор, направленный по касательной к траектории.

На практике зачастую интерес представляет только численное значение скорости. Его легко найти, когда закон движения задан в скалярной форме (1.2.3), продифференцировав его:

υ = 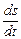(1.2.8)

Скорость будет выражаться положительным числом при движении тела по траектории в положительном направлении и отрицательным при движении в отрицательном направлении.

Когда закон движения задан в координатной форме (1.2.2), то следует найти проекции вектора скорости на координатные оси как первые производные по времени от соответствующих координат, а затем найти модуль вектора скорости:

υ _x=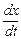, υ _y=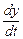, υ _z=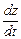, v=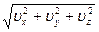 (1.2.9)

5. Ускорение 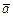характеризует быстроту изменения скорости. На рис. 4 показаны два положения на траектории движущейся частицы, соответствующие им скорост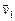и и 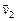, и приращение скорости 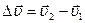. Вектор среднего ускорения

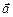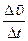<>= (1.2.10)

При уменьшении промежутка времени D t и стремлении его к нулю предел выражения (1.1.10) дает определение мгновенного ускорения:

(1.2.11)

Из рис. 4 следует, что при движении по криволинейной траектории вектор ускорения направлен под углом к вектору скорости внутрь траектории. При прямолинейном движении вектор ускорения совпадает с вектором скорости при ускоренном движении и противоположен ему при замедленном. Всякий вектор, в том числе и 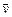, имеет две характеристики – модуль и направление, они могут изменяться независимо друг от друга. Используя формулы (1.2.7) и (1.2.11), получаем:

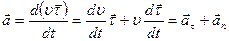(1.2.12)

Вектор ускорения состоит из двух слагаемых – тангенциального 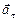и нормального 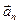ускорений. Первое слагаемое – тангенциальное ускорение – направлено по касательной к траектории и указывает на изменение модуля скорости. При убыстрении движения 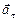и 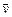направлены в одну сторону, при замедлении они противоположны. Величина тангенциального ускорения

a_t=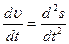 (1.2.13)

Второе слагаемое – нормальное ускорение – связано с изменением направления скорости. Это хорошо известное из школьного курса физики центростремительное ускорение при равномерном движении тела по окружности. Оно направлено по радиусу к центру окружности и равно:

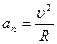(1.2.14)

R – радиус кривизны траектории, т.е. радиус соприкасающейся окружности, дугой которой можно заменить бесконечно малый участок кривой в окрестности данной ее точки. Задав в этой точке орт нормали 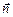, направленный по радиусу окружности в ее центр, получаем:

(1.2.15)

На рис 5 показан небольшой кусочек траектории, где в данный момент времени находится движущаяся частица. Орты касательный и нормали взаимно перпендикулярны, соответственно, перпендикулярны друг другу тангенциальное и нормальное ускорения, а полное ускорение равно:

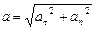(1.2.16)

Если закон движения задан в координатной форме, то модуль ускорения можно вычислить аналогично модулю скорости (формула 1.2.9) так:

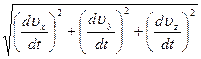= (1.2.17)

Для вычисления проекций вектора ускорения на оси координат можно воспользоваться формулами:

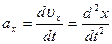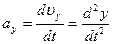, , (1.2.18)

§1.3. Равномерное и равнопеременное движения.

1. Взаимосвязь трех кинематических характеристик: закона движения, скорости и ускорения, рассмотренная в предыдущем параграфе, позволяет найти по одной известной кинематической характеристики остальные две. В предыдущем параграфе мы рассмотрели, как, зная закон движения, найти скорость и ускорение м. т. в любой момент времени. В этом параграфе рассмотрим решение обратной задачи кинематики: найти скорость как функцию времени и получить закон движения, зная зависимость ускорения от времени. Проделаем это на примерах равномерного и равнопеременного движений. Убедимся в том, что известные из школы формулы можно легко вывести, а не запоминать.

2. Равномерным называется движение, когда скорость не изменяется по величине, следовательно, тангенциальное ускорение a_t =0. Учитывая, что a_t=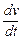, получаем: 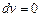, т.е. υ=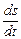= const. Находим первообразную (интегрируем) и получаем формулу равномерного движения:

s=s_o+υt (1.3.1)

Здесь s_o – координата тела на траектории в начальный момент времени t =0. Если начало отсчета совместить с начальным положением тела, то s_o= 0, и s = υt.

3. Равнопеременным называется движение с постоянным ускорением 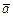= const. По аналогии с проделанным в предыдущем п.1, проинтегрируем формулы (1.2.11) и (1.2.6):

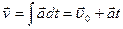(1.3.2)

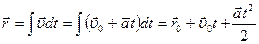(1.3.3)

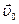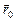В этих формулах и - начальная скорость и начальный радиус-вектор м.т (при t =0).

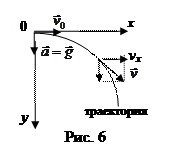4. Примером равнопеременного движения является свободное падение тела, при этом тело движется с ускорением свободного падения g= 9,8 м/с², направленным отвесно вниз к земле. Рассчитаем траекторию свободного падения тела, брошенного горизонтально с некоторой высоты над поверхностью земли. Тело движется в вертикальной плоскости и имеет две степени свободы, так что нарисуем две оси декартовых координат, поместив начало отсчета в точку старта тела. Ось x направим горизонтально, ось y направим вертикально вниз (рис.6). Закон движения тела имеет вид (1.3.3), причем, r₀= 0,вектор начальной скорости 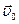направлен по оси х. Запишем этот закон в проекциях на оси координат:

x=υ₀t

y=gt²/2.

Мы получили уравнение траектории (линии), заданное параметрически. Выразим из первого уравнения t, подставим его во второе: у=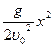. Итак, при свободном падении тело летит по параболе. На практике такому движению мешает сопротивление воздуха, так что полученный нами результат приближенный.

§ 1.4. Кинематика вращательного движения.

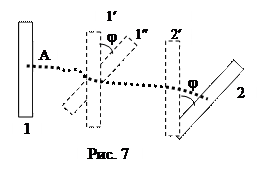Абсолютно твердое тело (а.т.т.) - еще одна модель механики. Она учитывает размеры и форму тела, но пренебрегает их изменением при движении, т.е. деформациями. А.т.т. можно считать системой материальных точек, взаимное расположение которых не изменяется. Любое движение а.т.т. можно представить как сумму поступательного и вращательного движений. При поступательном движении все точки тела имеют одинаковые скорости и одинаковые ускорения в любой момент времени. При вращательном движении траектории всех точек тела – окружности, их плоскости совпадают или параллельны друг другу, а центры лежат на одной прямой (ее называют ось вращения). На рис. 7 представлены два положения движущегося твердого тела, они обозначенные числами 1 и 2. Траектория движения некоторой точки А тела указана пунктиром. Перемещение тела из положения 1 в положение 2 может быть осуществлено разными способами. Две возможных комбинации поступательного и вращательного движений показаны промежуточными положениями тела. Первый вариант: сначала поступательное движение 1®1¢, затем вращательное 1¢®1¢¢, и опять поступательное 1¢¢®2. Второй вариант: сначала поступательное движение 1®2¢, затем вращательное 2¢®2. Можно рассмотреть еще множество разных вариантов, но в любом из них угол поворота тела j будет один и тот же, а вот скорость поступательного движения может быть различной.

Из рассмотренного ясно, что поступательное движение тела сводится к движению точки. Освоив кинематику вращательного движения, мы сможем справиться с кинематикой произвольного движения тела.

2. На рис.8 показано а.т.т. произвольной формы, вращающееся вокруг вертикальной оси, закрепленной в неподвижных подшипниках, изображенных скобочками. Указаны траектории движения двух точек тела. Радиусы и плоскости окружностей, описываемых этими точками, различны, а вот центральные углы, на которые опираются дуги, описанные разными точками при вращении тела, одинаковы. Из этих рассуждений следует, что вращающееся тело имеет всего одну степень свободы: i =1. Его положение в пространстве задает одна координата - угол поворота тела j относительно некоторого положения, выбранного за начало отсчета. Закон вращательного движения выражает уравнение

j = j (t) (1.4.1)

Разность угловых координат в конечный t₂ и начальный t₁ моменты времени равна пути при вращении, измеряемом углом Dj = j₂ - j₁. Малые угловые перемещения (Dj <<2p) можно считать векторами[2], будем их обозначать . Этот вектор направлен вдоль оси в соответствии с правилом правого винта, т.е. указывает направление вращения тела, и не имеет фиксированной точки закрепления. Такой вектор называется аксиальным (осевым) в отличие от полярных векторов ,,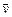 , 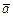рассмотренных нами в § 1.2.

Быстроту вращения характеризует угловая скорость w.

Средняя угловая скорость

<w>=Dj / Dt (1.4.2)

Мгновенная угловая скорость

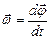(1.4.3)

Быстроту изменения угловой скорости описывает угловое ускорение e. Его среднее значение

< e > = Dw / Dt (1.4.4)

Мгновенное угловое ускорение

(1.4.5)

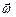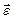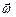и - аксиальные векторы, направленные вдоль оси, как и . Направление вектора угловой скорости определяет правило правого винта, а направление вектора углового ускорения зависит от знака изменения угловой скорости: при ускоренном вращении и 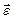направлены вдоль оси в одну сторону, при замедленном – в противоположные стороны. В СИ угловая координата измеряется в радианах (рад), угловая скорость в рад/с, угловое ускорение в рад/с².

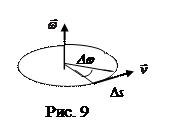3. Найдем связь между линейными и угловыми кинематическими характеристиками точки вращающегося тела. На рис. 9 показана траектория некоторой точки тела, отстоящей от оси вращения на расстоянии R, ее линейная скорость 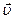и угловая скорость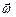. За промежуток времени Dt тело повернулось на угол Dj, а точка прошла путь Ds. Очевидно, Ds=RDj. Исходя из определений линейной и угловой скоростей (формулы 1.2.8 и 1.4.3) получаем:

υ=wR (1.4.6)

Используя формулы (1.2.13) и (1.2.15), получаем:

a_t = e R (1.4.7)

a_n=w ²R (1.4.8)

Обратите внимание, что нормальное ускорение всегда бывает у точек вращающегося тела, а тангенциальное только при неравномерном вращении.

§ 1.5. Краткие итоги главы 1.

Проследим аналогию кинематических характеристик и формул поступательного и вращательного движений.

Поступательное Вращательное

Координата s j

Путь Ds Dj

Скорость средняя < υ > =Ds / Dt <w>=Dj / Dt

Скорость мгновенная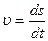

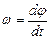
Ускорение среднее < a >= Dυ / Dt <e>=Dw / Dt

Ускорение мгновенное a_t=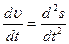

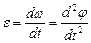
Равномерное движение

a_t= 0 e=0

υ= const w = const

s=s₀+vt j =j₀+w t

Равнопеременное движение

a_t= const e=const

υ=υ₀+a_t t w =w₀+e t

s=s₀+υ₀ t+at²/ 2 j =j₀+w₀ t+e t² /2

Подводя итог изучения Главы 1 «Кинематика», еще раз заметим, что, рассматривая движение конкретного физического тела, следует использовать такую последовательность:мы

1. выбрать систему отсчета,

2. заменить тело соответствующей моделью, сделать рисунок, поясняющий задачу,

3. определить число степеней свободы и характер движения тела и только после этого вспоминать и искать формулы.

§ 2.1.Задача динамики. Состояние материальной точки. Динамические характеристики движения.

1. Задача динамики – найти закон движения тела, если известно, каким внешним воздействиям оно подвергается, или, наоборот, найти, каким внешним воздействиям должно подвергаться тело, чтобы выполнялся заданный закон движения. Для теоретического решения такой задачи необходимо уметь: а) задать динамическое состояние тела, б) задать внешнее воздействие, в) составить и решить уравнение динамики. Подтверждением справедливости теории является совпадение ее результатов с опытом.

2. Опыт показывает, что состояние м.т. определено, если известен ее радиус – вектор 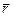и скорость 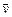. Нам это кажется очевидным, однако понимание этого появилось только в эпоху Ньютона. Еще Аристотель удивлялся тому, что топор, приставленный к полену, не оставляет на нем даже следа, а топор, с размаху ударяющий по полену, раскалывает его. Одно и то же положение топора – соприкосновение с поленом – соответствует разным его состояниям, потому что различаются его скорости. Поэтому неудивительно, что разные состояния в начальный момент ведут к разным результатам. Индивидуальной динамической характеристикой м.т. является ее масса m, так что более информативные параметры состояния м.т. - 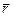и импульс 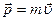(его устаревшее название – количество движения). В СИ единицей измерения импульса является 1 кг^. м/с.