Конспект лекций 6 страница

§ 6.6. Энтропия.

1. Энтропия (от греч. поворот, превращение) является функцией состояния термодинамической системы в том же смысле, что и внутренняя энергия. Это значит, что каждому состоянию термодинамической системы соответствует определенное значение энтропии. При переходе системы из одного состояния в другое изменение энтропии одинаково для любых процессов, связывающих эти два состояния, а в цикле изменение энтропии равно нулю. Рассмотрим цикл Карно. Его КПД может быть выражен так: h=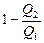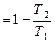, откуда следует: 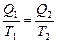, и далее: 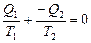. Напомним, что тепло – алгебраическая величина. Q <0 означает, что у тела «забирают» тепло, т.е. оно получает отрицательное количество тепла. Количество тепла, изотермически сообщенное телу, деленное на температуру, называют приведенным количеством тепла. В цикле Карно приведенное количество тепла равно нулю. В предыдущем параграфе мы отмечали, что любой обратимый цикл можно рассматривать как сумму элементарных циклов Карно, следовательно, в любом обратимом цикле приведенное количество тепла равно нулю. При элементарном изменении состояния приведенное количество тепла выразится формулой: 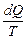, и приведенное количество тепла в обратимом цикле[20]:

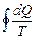=0 (6.6.1)

Полученная формула показывает, что термодинамическая система характеризуется некоторой функцией состояния, изменение которой равно приведенному количеству тепла. Эту функцию состояния называют энтропией и обозначают S. Ее изменение в элементарном процессе 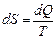. При переходе из состояния 1 в состояние 2 изменение энтропии

D S=S ₂- S ₁=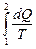 (6.6.2)

Найдем формулу энтропии идеального газа. Подставим в формулу (6.6.2) формулу первого начала термодинамики для идеального газа:

D S= 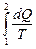=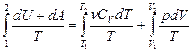. Интегрирование с учетом уравнения состояния идеального газа 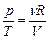дает:

D S=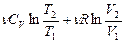 (6.6.3)

Из (6.6.3) следует формула энтропии идеального газа:

S=S₀ +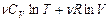 (6.6.4)

Здесь S₀ – некоторая постоянная.

2. Выясним физический смысл энтропии. На примере идеального газа мы убедились, что энтропия в каждом состоянии тела имеет определенное значение, и, подобно энергии, является функцией состояния. Энергия характеризует способность тела совершать работу и может быть запасена в виде внутренней энергии термодинамической системы. Рассматривая цикл Карно, мы увидели, что внутренняя энергия нагревателя тем эффективнее превращается в работу, чем больше перепад температур нагревателя и холодильника. Если их температуры одинаковы, то КПД равен нулю, и внутренняя энергия не может работать. Напомним, что в равновесной термодинамической системе температура во всех ее областях одинакова. Следовательно, равновесная термодинамическая система может иметь большой запас внутренней энергии, но совершать механическую работу не может. Говорят, что энтропия – мера «обесцененности» внутренней энергии. Знание энтропии позволяет судить о том, можно ли внутреннюю энергию использовать для совершения работы. Мы уже отмечали, что работать может только неравновесная термодинамическая система. Таким образом, энтропия – мера приближения термодинамической системы к равновесию. Термодинамическое равновесие означает полнейшую идентичность друг другу разных участков системы, т.е. ее полную «хаотизацию», следовательно, энтропия – мера «хаотизации». Больцман, используя статистический метод, получил формулу энтропии в виде:

S=к lnW (6.6.5)

к – постоянная Больцмана, W – термодинамическая вероятность состояния системы, она равна числу микросостояний, каким может быть получено данное макросостояние. Поясним смысл этих

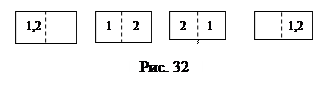
понятий на примере газа. Макроскопическое состояние газа определяют его параметры состояния: давление, объем, температура. Микроскопическое состояние определяется состоянием каждой его конкретной молекулы, т.е. ее положением в пространстве и скоростью. При тепловом движении молекул их состояния меняются хаотически, а состояние газа остается неизменным. Для примера рассмотрим сосуд, в котором содержатся 2 молекулы, каждая из которых может находиться в одной из половинок сосуда, т.е. каждая молекула имеет 2 микросостояния. Пронумеруем молекулы и распределим их в сосуде согласно возможностям хаотического движения. На рис. 32 показан сосуд и молекулы в нем в разных микросостояниях. Общее число микросостояний W, соответствующих данному макросостоянию – в сосуде содержится две молекулы - равно 4, т.е. W =2²=4. Заметим, что в равновесном состоянии системы, когда молекулы равномерно распределены по объему, W= 2, а каждому неравновесному состоянию системы – обе молекулы собрались в правой или в левой половине сосуда – соответствует по одному микросостоянию. Добавляя по одной молекуле в сосуд и увеличивая их число до N, получим: W= 2^N, причем, равновесному макросостоянию всегда соответствует наибольшее число возможных микросостояний. Мы получили еще один результат: состоянию термодинамического равновесия, когда система, обладая энергией, не может совершать работу, соответствует наибольшая термодинамическая вероятность, а вместе с ней и наибольшая энтропия. В состоянии термодинамического равновесия энтропия максимальна, и максимально «обесценена» внутренняя энергия.

§ 6.7. Второе начало термодинамики.

1. Из опыта мы знаем, что нагретые тела самопроизвольно остывают, а холодные, наоборот, самопроизвольно нагреваются, до температуры окружающей среды. При нагревании внутренняя энергия тела увеличивается, при охлаждении уменьшается. Если горячему телу сообщить дополнительную энергию, забрав соответствующее количество внутренней энергии у холодного тела, то температура горячего тела повысится, а холодного понизится. Такой процесс не противоречит первому началу термодинамики, в нем выполняется закон сохранения энергии. Но такие процессы самопроизвольно не происходят, они запрещены законом природы, который называется вторым началом (законом) термодинамики. Этот закон констатирует, что тепловые процессы в замкнутой системе идут только в определенном направлении, а именно, тепло самопроизвольно передается от горячего тела к холодному. С действием второго закона термодинамики мы постоянно встречаемся в повседневной жизни, примером являются нагретые батареи системы отопления.

2. Существуют другие математически эквивалентные формулировки второго начала термодинамики. Приведем некоторые из них.

· Никакая тепловая машина периодического действия не может иметь КПД, превышающий (Т ₁ -Т ₂)/ Т ₁, где Т ₁и Т ₂ – соответственно наибольшая и наименьшая температуры в цикле.

· Невозможен вечный двигатель второго рода.

· Энтропия замкнутой системы не может убывать: D S³ 0.

Первую из приведенных формулировок второго начала термодинамики мы уже обсудили в § 6.5.

Обсудим вторую формулировку. Вечным двигателем первого рода называется машина, которая производит работу без всякого внешнего источника энергии. Вечный двигатель первого рода имеет только рабочее тело, а нагреватель и холодильник в ней отсутствуют. Рабочее тело является замкнутой системой, и его состояние циклически изменяется. Такое устройство противоречит закону сохранения энергии. Невозможность создания вечного двигателя первого рода есть еще одна формулировка первого начала термодинамики. Вечный двигатель второго рода представляет собой циклически работающую машину, которая, получая тепло от внешнего источника энергии, целиком превращает его в механическую работу и имеет КПД 100%. У этой машины есть нагреватель и рабочее тело, но нет холодильника. Ранее мы уже убедились, что циклическое превращение тепла в механическую работу требует три обязательных тела: нагреватель, рабочее тело и холодильник.

Обсудим третью формулировку. Мы подошли к этому утверждению, рассматривая понятие энтропии в предыдущем параграфе. Действительно, если в замкнутой системе нет термодинамического равновесия, то вследствие теплового движения оно рано или поздно установится. Если замкнутая система уравновешена, то это ее состояние не может измениться без внешнего воздействия, а по определению замкнутой системы такого воздействия быть не может. Состоянию термодинамического равновесия соответствует наибольшая термодинамическая вероятность W и максимальное значение энтропии (см. формулу 6.6.5). Таким образом, если в результате предполагаемого процесса энтропия замкнутой системе уменьшится, то заведомо ясно, что такой процесс невозможен.

Тепловые процессы статистические, они происходят в результате хаотического, случайного движения частиц. Легко представить, что следствием случайностей может быть небольшое нарушение равновесия, например, в некоторый момент времени число частиц в одной половине сосуда может оказаться немного больше, или, наоборот, немного меньше, чем в другой. Такие самопроизвольные отклонения от положения равновесия называются флуктуациями. Понятно, что вероятность малых флуктуаций велика, а вероятность больших флуктуаций мала. При возникновении флуктуации нарушается термодинамическое равновесие, и энтропия уменьшается. Следовательно, в замкнутой системе возможны процессы, энтропия которых немного уменьшается. Учет статистического характера тепловых процессов отменяет категоричность ранее приведенной формулировки второго начала термодинамики. Ее более точная формулировка имеет вид: в замкнутой термодинамической системе наиболее вероятными являются такие процессы, в результате которых энтропия не уменьшается, т.е. D S³ 0.

3. Направленность тепловых процессов, о которой говорит второе начало термодинамики, связана с необратимостью реальных физических процессов. Чисто механические процессы, когда нет сил трения, обратимы. Например, выпущенный из рук мячик падает на пол, его потенциальная энергия превращается в кинетическую. После упругого удара мяч отскакивает и движется вверх, причем, обратный процесс складывается из последовательности тех же состояний, но проходимых в обратной последовательности, что и прямой путь. В процессе движения мяча происходит превращение механической энергии тела как целого из одного вида в другой, и это никак не отражается на внутреннем состоянии тела как совокупности частиц.

В термодинамических процессах участвует огромное число частиц, образующих тело. Принципиально необратимы процессы, в которых участвует большое число хаотически движущихся частиц: расширение газа в пустоту и теплопередача от горячего тела к холодному. Процесс расширения газа в пустоту выглядит так: одну половину сосуда, разделенного перегородкой на две части, заполним газом; после снятия перегородки молекулы необратимо разлетятся по всему сосуду. В § 6.2 мы отмечали, что при передаче тепла происходит передача энергии от «горячих» частиц к «холодным» путем непрерывного совершения микроскопической работы. Подобный механизм хаотического перераспределения энергии сопровождает действие силы трения. Работа этой силы приводит к уменьшению механической энергии тела: она превращается в тепло и перераспределяется между отдельными частицами тела, увеличивая «хаотизацию». Поясним рассмотренный механизм понятным примером из повседневной жизни. Если Вы дали деньги в долг своему надежному товарищу, то процесс обратим – деньги вернутся. Если же Вы вытащили из своего кармана некую сумму и бросили ее в толпу – процесс необратим. Во всех реальных процессах всегда присутствует рассмотренный механизм, и все реальные процессы необратимы, они приближают систему к положению равновесия. Полностью «хаотизированная», т.е. равновесная система неработоспособна. Вся наша разумная деятельность направлена на уменьшение «хаотизации» в локальной области незамкнутой системы.

Как показало развитие науки, Вселенная является незамкнутой системой, и гипотеза о «тепловой смерти Вселенной», возникшая в науке более века назад, несостоятельна. Суть этой гипотезы такова. В замкнутой системе самопроизвольно наступает полный хаос, и температура во всех ее частях и прочие термодинамические параметры выравниваются. Источником жизни на Земле является Солнце. Установление теплового равновесия во Вселенной означает возникновение всеобщего молекулярного хаоса и прекращение всякого направленного движения, которым является жизнь. Мы уже не раз отмечали, что все физические законы имеют определенную область применения. Незамкнутость термодинамической системы означает неприменимость к ней второго начала термодинамики.

§ 6.8. Основные выводы главы 6.

1. Термодинамические процессы и их законы используются в тепловых и холодильных машинах, без применения которых немыслима современная техника.

2. Термодинамический метод рассмотрения свойств любых тел, которые являются термодинамическими системами, широко применяется при изучении разных физических явлений и объектов.

3. Термодинамическая система является статистической, и механизм происходящих в ней явлений носит статистический характер.

Раздел 3. Электромагнетизм

§7.1.Электрический заряд. Закон Кулона.

В основе всего разнообразия явлений природы лежат четыре фундаментальных взаимодействия: сильное, электромагнитное, слабое и гравитационное. В механике мы уже упоминали, что гравитационное взаимодействие проявляет себя силой тяжести, а упругая сила и сила трения есть проявление электромагнитного взаимодействия. Каждый вид взаимодействия связан с определенной характеристикой частицы. Так, гравитационное взаимодействие связано с массой, а электромагнитное с электрическим зарядом частицы. Электрический заряд частицы является одной из основных, первичных ее характеристик. Перечислим фундаментальные свойства заряда:

1. Знак - существуют положительные и отрицательные заряды.

2. Квантование – заряд любой частицы (тела) равен целому числу элементарных зарядов; величина элементарного заряда в единицах СИ составляет 1,6^.10¹⁹ Кл; электрон имеет элементарный отрицательный заряд, протон - элементарный положительный заряд.

3. Релятивистская инвариантность – величина заряда не зависит от скорости его движения и одинакова в любой инерциальной системе отсчета[21].

4. Закон сохранения заряда – в любой электрически изолированной (замкнутой) системе частиц алгебраическая сумма зарядов не изменяется.

5. Закон Кулона выражает силу взаимодействия двух точечный зарядов.

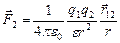
(7.1.1)

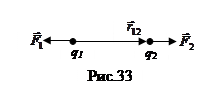Точечным зарядом называется заряженная частица, к которой применима модель материальной точки. Рис. 33 иллюстрирует закон Кулона: показаны два точечных заряда на расстоянии и их силы взаимодействия. 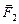-вектор силы, действующей на второй заряд со стороны первого, 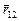- вектор, проведенный из точки, где находится первый заряд, в точку, где находится второй заряд. Модуль этого вектора равен расстоянию между зарядами: r= ç ç. Отметим, что закон Кулона, как и закон всемирного тяготения, утверждает, что сила взаимодействия обратно пропорциональна квадрату расстояния между частицами. Однако, гравитационное взаимодействие всегда есть притяжение масс, тогда как одноименные заряды отталкиваются, а разноименные притягиваются. 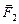Это отражено в формуле (7.1.1): произведение одноименных зарядов дает положительное число, и векторы и 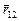направлены одинаково, заряды отталкиваются. Произведение разноименных зарядов дает отрицательное число, в этом случае векторы 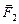и 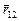направлены противоположно друг другу, а заряды притягиваются. В соответствии с третьим законом Ньютона F₁=F₂=F. В скалярной форме закон Кулона имеет вид:

F=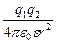 (7.1.2)

e₀ – электрическая постоянная, зависит от выбора системы единиц, в СИ e₀= 8,85^.10¹² Ф/м. e - безразмерная величина, диэлектрическая постоянная, индивидуальная характеристика свойств диэлектрика. Она показывает, во сколько раз сила взаимодействия зарядов в диэлектрике меньше, чем в вакууме, при прочих равных условиях. Позже мы выясним ее физический смысл. Отметим, что в воздухе e = 1.

§7.2. Электрическое поле. Напряженность.

1. Взаимодействие частиц на расстоянии в физике описывают с помощью особого вида материи – силового поля. Примером является гравитационное поле: оно создается частицей, имеющей массу, и действует на другую частицу, помещенную в гравитационное поле и обладающую массой. Аналогичным образом можно рассматривать взаимодействие частиц, обладающих зарядами. Заряд изменяет свойства окружающего его пространства, создавая в нем электрическое поле. Обнаруживает себя это поле силой, действующей на другой заряд. Рассмотрим закон Кулона (формула 7.1.1). Будем считать, что первый заряд создает поле, и это поле действует на второй заряд, причем, 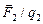зависит только от источника поля, и от положения точки поля относительно источника, т.е. является силовой характеристикой поля. Можно сказать, что поле первого заряда бдительно следит за появлением «чужака», и, как только он где-либо в поле появится, тут же действует на него соответствующей силой. Этот способ описания взаимодействия зарядов абсолютно симметричен: можно считать, что второй заряд создает поле, а это поле действует силой на первый заряд. Силовая характеристика электрического поля называется напряженностью, обозначается 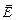, в СИ измеряется в вольтах на метр (В/м). На посторонний заряд q поле действует силой

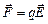(7.2.1)

Поле, созданное неподвижными зарядами, называется электростатическим. Напряженность поля точечного заряда q в точке, заданной вектором 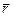, проведенным из заряда (см. формулу 7.1.1):

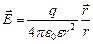(7.2.2)

Вектор напряженности электростатического поля точечного заряда направлен вдоль прямой, соединяющей точку, где находится заряд, с данной точкой поля. Он выходит из точки поля и направлен от заряда, если он положительный, и к заряду, если он отрицательный. Величина напряженности

E=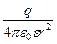 (7.2.3)

Пусть имеется система точечных зарядов q_i (i= 1, 2, …). Поместим в некоторую точку системы, положение которой относительно каждого ее заряда указывает вектор 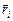, посторонний заряд q. На него со стороны каждого заряда системы действует кулоновская сила. Их равнодействующая:

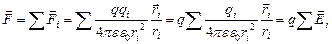(7.2.4)

Полученный результат называется принципом суперпозиции (независимого сложения) электрического поля: если имеется несколько источников, то каждый из них создает свое поле независимо от всех прочих, и эти поля, складываясь, дают результирующее поле[22]. Формула принципа суперпозиции такова:

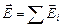(7.2.5)

2. Поле известно, если известен вектор напряженности в каждой точке. Электрическое поле можно изображать графически векторами напряженности. Этот способ удобен для изображения поля в отдельных точках. Если поле надо нарисовать в некоторой области пространства, то используют линии напряженности (их называют еще силовыми линиями). Касательная к силовой линии указывает направление 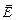в данной точке поля, густота (плотность) силовых линий вблизи этой точки равна величине напряженности. Силовые линии электростатического поля выходят из положительного заряда и входят в отрицательный заряд.

На рис. 34 показаны силовые линии поля положительного и отрицательного точечных зарядов, поля диполя, а также области некоторого электростатического поля - образующие его заряды находятся вне рассматриваемой области.

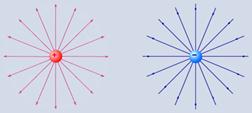
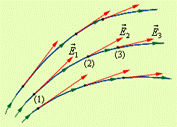
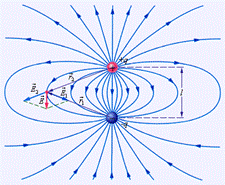
Рис. 34

Диполь – два точечных разноименных зарядов одинаковой величины. На рис. 34 в одной из точек поля диполя показано построение вектора напряженности с помощью принципа суперпозиции. Силовые линии – воображаемые, но их можно сделать видимыми (вспомните лекционные демонстрации).

§ 7.3. Теорема Гаусса.

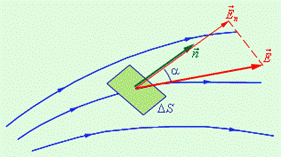1. Принцип суперпозиции позволяет рассчитать электрическое поле, созданное любыми заряженными телами, рассматривая их как систему точечных зарядов. Иногда это сопряжено с заметными математическими трудностями. Поле, созданное симметричным распределением зарядов, значительно легче рассчитать, используя теорему Гаусса. Ее формулировка использует понятие потока вектора напряженности через поверхность. Поток вектора – скалярная величина, он равен числу силовых линий, пересекающих эту поверхность. На рис. 35 силовыми линиями изображено электростатическое поле, в котором находится плоская поверхность площадью DS. Ее пространственную ориентацию указывает нормаль 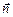, образующая с 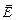угол a. Поток через эту элементарную поверхность равен EDScosa. = E_nDS. Из определения ясно, что поток положительный, если 0£ a < 90⁰ (силовые линии входят в поверхность); поток отрицательный, если 90⁰£ a <180⁰(силовые линии выходят из поверхности); поток равен нулю, если a =90⁰ (силовые линии скользят по поверхности, не пересекая ее).

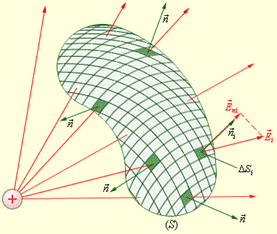Теперь найдем поток через замкнутую поверхность произвольной формы (рис.36). Разобьем эту поверхность на элементарные участки площадью dS (на рисунке они обозначены DS), найдем элементарные потоки и просуммируем их по всей поверхности. Заметим, что в любой точке замкнутой поверхности нормаль принято направлять наружу. Поток через замкнутую поверхность обозначают так: 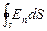. Кружок на интеграле указывает, что поверхность замкнутая. Заметим, что на нашем рисунке поток равен нулю: число входящих в поверхность силовых линий равно числу выходящих из нее, линии насквозь проходят через поверхность. Вспомним, что силовые линии электрического поля начинаются и заканчиваются на зарядах, т.е. источниками и стоками потока являются заряды. Понятно, что если внутри замкнутой Рис 36 поверхности нет зарядов, то поток через нее равен нулю. Поток – это разность числа входящих в поверхность и выходящих из нее силовых линий. Мысленно деформируйте или переместите на новое место поверхность на рис. 36. Поток через нее всегда равен нулю, если заряд находится снаружи. Если заряд окажется внутри, то поток через поверхность любого размера и формы один и тот же. Это и есть содержание теоремы Гаусса: поток вектора напряженности электростатического поля в вакууме через любую замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности, деленной на электрическую постоянную:

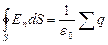(7.3.1)

2. Рассмотрим примеры применения теоремы Гаусса.

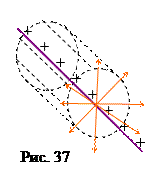а) Поле однородно заряженной бесконечной нити. На рис. 37 показан отрезок нити (фиолетовая линия), на нити равномерно распределен заряд (его обозначили знаками «плюс»). На каждом элементе длины dl содержится заряд dq, линейная плотность заряда t = dq/dl= const. Понятно, что поле обладает цилиндрической симметрией. Это значит, что линии напряженности (оранжевые векторы) направлены по радиусам прямого цилиндра, ось которого совпадает с нитью. В качестве замкнутой поверхности рассмотрим часть такого прямого цилиндра радиусом r и длиной l, на рисунке он показан пунктирными линиями. Силовые линии пересекают боковую поверхность цилиндра по нормали, создавая поток ES _бок= E 2p rl, и скользят вдоль оснований цилиндра, не создавая потока сквозь них. Суммарный заряд, заключенный внутри этой поверхности q=tl. Подставляя эти результаты в формулу (7.3.1), получаем:

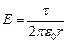(7.3.2)

б) Бесконечная однородно заряженная плоскость. Поверхностная плотность заряда s=dq/dS= const. Из соображений симметрии ясно, что силовые линии равномерно выходят из плоскости перпендикулярно к ней в обе стороны, если плоскость заряжена положительно, и входят в нее, если заряд плоскости отрицательный. (Сделайте рисунок самостоятельно). С каждой стороны плоскости линии напряженности направлены в противоположные стороны, но густота их одинакова. В качестве замкнутой поверхности выберем поверхность прямого цилиндра, образующие которого перпендикулярны заряженной плоскости, а основания параллельны ей. Силовые линии скользят по его боковой поверхности и пересекают оба основания параллельно нормали к каждому основанию. Суммарный поток равен 2 ES. Суммарный заряд, находящийся внутри поверхности, q=ES. Из теоремы Гаусса получаем:

E=s /2 e₀ (7.3.3)

в) Плоский конденсатор. Он образован двумя бесконечными разноименно заряженными плоскостями с одинаковой плотностью зарядов: s ₊= s_- = s = const (рис. 38).На рисунке обозначены заряды плоскостей и нарисовано по одной силовой линии полей этих зарядов. Согласно принципу суперпозиции 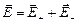, так что

E=s / e₀ , внутри конденсатора (7.3.4)

Е= 0, снаружи конденсатора (7.3.5)

Плоский конденсатор является источником однородного электрического поля, во всех точках которого векторы напряженности одинаковы, а силовые линии – параллельные прямые, проведенные с равномерной плотностью, при этом поле сосредоточено в пространстве между пластинами. Разумеется, реальный плоский конденсатор имеет пластины конечных размеров, и вблизи его краев поле неоднородное. Но чем меньше разница между расстоянием между пластинами и линейным размером пластин, тем точнее электростатическое поле в центральной части объема конденсатора соответствует однородному. На практике для получения однородного поля используют плоский конденсатор.

г) Поле равномерно заряженной сферы. Из соображений симметрии ясно, что силовые линии – радиальные прямые[23]. Такое поле называется сферически симметричным. Легко посчитать поток через любую сферическую поверхность радиуса r, центр которой совпадает с центром заряженной сферы: 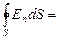ES=E 4p r². Если радиус поверхности интегрирования равен или больше радиуса сферы R (r ³ R), то находящийся внутри поверхности интегрирования заряд равен заряду сферы q. Если r < R, то внутри поверхности интегрирования нет заряда. Применяя теорему Гаусса, получаем: равномерно заряженная сфера снаружи создает такое же поле, как точечный заряд, помещенный в ее центр (см. формулы 7.2.2 и 7.2.3); внутри сферы поля нет, Е=0.