Интегрирование рациональных дробей. Интегрирование рациональных выражений

Лекция 6

Интегрирование рациональных выражений.

Рациональное выражение: ∫ P(x)/ Q(x) dx, P(x), Q(x) многочлены от Х.

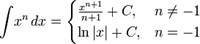
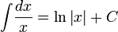
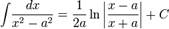
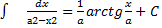
Пример:

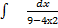= -1/4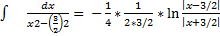+С= -1/12 * =

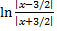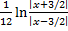
Выносим постоянный множитель – ¼

Пример:

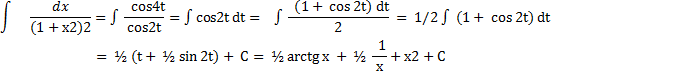
Подстановка x= tg x, dx= d tg x=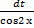

1+x²= 1+ tg ²t= 1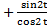= sin²t+ cos²t / cos²t=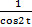

1/ (1+x²) ²=1/ 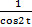²=cos⁴t

cos² t =(1+ cos 2t)/2

sin 2t= 2 tg t / (1+ tg² t)= 2x/ 1+x²

Пример:

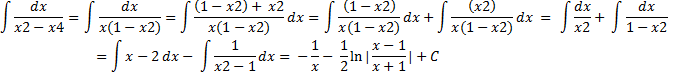
ПРИМЕР 1:

Дискриминант знаменатель больше 0:

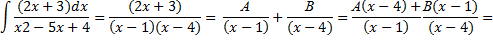
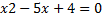
D=25-4*4=9

√D=3

X1=

X2=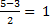

(x-4)(x-1)

2x+3=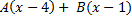

При х=1: 5= -3А à А=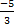

При х=4: 11= 3В à В=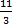

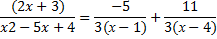
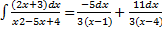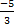= ln | x-1| + 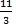ln | x-4|+С= (11 ln | x-4|- 5 ln|x-1|)+C=

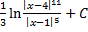
ПРИМЕР 2:

Знаменатель имеет одинаковые кратные корни:

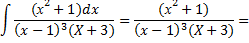
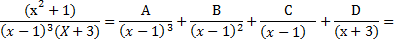
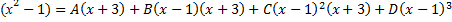
При х=1: 2=4А à А=

При х = -3: 10= -64D à D=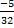

Сравним коэффициенты при старшей степени левые и правые части.

При х^3: 0 = С+D

При х=0: 1= 3A-3B+3C-D

C= -D=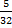

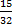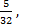1= – 3B+ + B=

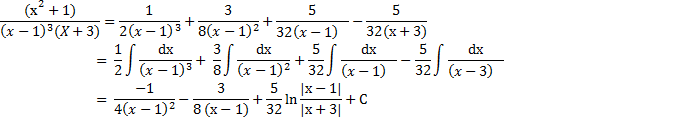
ПРИМЕР 3:

В знаменателе имеются простые комплексные корни.

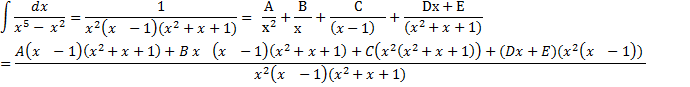
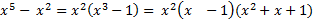
D= 1-4 < 0

1= A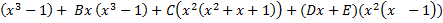

При х=0: 1= -1А A= -1

При х=1: 1= 3C C=

Остается решить систему: