Метод интегрирование по частям

Лекция 4.

Пусть u=u(x) и v=v(x) дифференцируемые функции, тогда справедлива формула интегрирования по частям:

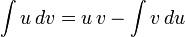
В качестве u целесообразно выбрать функцию, которая при дифференцировании упрощается.

На практике u=xⁿ, u=ln x, u=arcsin x, u-arccos x, u=arctg x, u= arcctg x.

Пример:

∫ ln x dx= x lnx-∫ x dx= x lnx ∫ dx= x lnx-x+C

Предположим, что du=dx

U=ln x,

Du=d(ln x)= dx

V= ∫ dv= ∫dx= x+C=x, считаем, что С=0, v=x

Пример:

∫ x sin xdx= - x cos x- ∫ -cos xdx= -xcos x + sin x+C

Предположим, что u=x, тогда

du= sinx dx

du=dv

v= ∫ dv= ∫ sin x dx= -cos x

Пример:

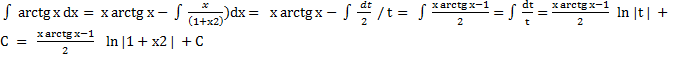
Предположим, что u= arctg x

Du= dx,

d arctg x=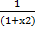dx= du

V=x

Применим подстановку

1+ x²= t

dt= d(1+x²)= 2 x dx, xdx=