Если ф-ция 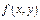 или
или 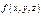 непрерывна, а кривая на отрезке
непрерывна, а кривая на отрезке  непрерывна и имеет непрерывно вращающуюся касс-ную, то кривол-й интеграл 1-го рода типа (А) или (Б) сущ-ет. Т. е. пределы сущ-ют и не зависят от выбора точек
непрерывна и имеет непрерывно вращающуюся касс-ную, то кривол-й интеграл 1-го рода типа (А) или (Б) сущ-ет. Т. е. пределы сущ-ют и не зависят от выбора точек 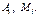
Вычисление криволинейного интеграла 1-го рода. Оно сводится к вычислению опред-го интеграла:
1) Если ур-ия пути интегрирования заданы в парам-й форме 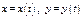 (для пространственной кривой
(для пространственной кривой  ), то
), то
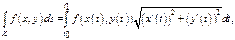 (А)
(А)
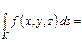
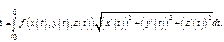 (Б)
(Б)
Здесь знач-е пар-ра 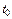 берется для точки
берется для точки 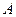 , знач-е пар-ра
, знач-е пар-ра 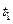 берется для точки
берется для точки  . Точки
. Точки 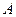 и
и  выбираются так, чтобы выполнялось нер-во
выбираются так, чтобы выполнялось нер-во 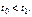
2) Если ур-я пути интегр-я заданы в явном виде 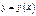 для плоской кривой (для простр-й кривой
для плоской кривой (для простр-й кривой 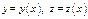 ), то
), то
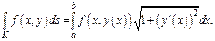 (А)
(А)
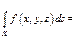
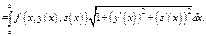 (Б)
(Б)
Здесь знач-е 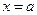 берется для точки
берется для точки 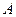 , знач-е
, знач-е 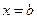 берется для точки
берется для точки  . Точки
. Точки 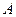 и
и  выбир-ся так, чтобы выполнялось нер-во
выбир-ся так, чтобы выполнялось нер-во 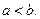
Замечание. Пусть кривая такова, что для заданного 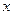 координата
координата  принимает несколько значений, например:
принимает несколько значений, например:

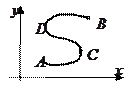
Тогда кривую нужно разбить промеж-ми точками на отрезки таким образом, чтобы для каждого отрезка выполнялось взаимно однозначное соотв-вие между 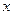 и
и  , и интегрировать в сторону увеличения корд-ты
, и интегрировать в сторону увеличения корд-ты 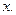 Для данного примера криволинейный интеграл 1-го рода примет вид
Для данного примера криволинейный интеграл 1-го рода примет вид
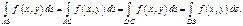
 2014-02-02
2014-02-02 298
298








