Понятие длины дуги кривой. Диф-ал длины дуги. Криволин-й интеграл 1 рода (по длине дуги). Св-ва, вычисление, применения

Приложения тройных интегралов.

Пусть дано тело 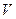переменной плотности . Массу тела 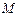можно вычислить по формуле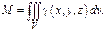

1) Статич-е моменты инерции тела относ-но коорд-х плоск-й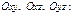

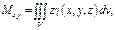
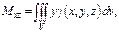
2) Координаты центра тяжести:

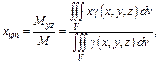
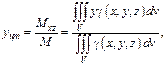
Если тело однородно, т. е. 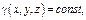то

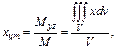
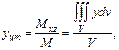
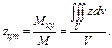
3) Моменты инерции тела относи-но коорд-х осей:

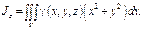
4) Центробежные моменты инерции тела:

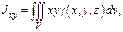
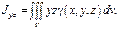
5) Полярный момент инерции тела:

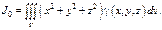
Криволинейный интеграл по длине (1 – го рода).

Диф-ал длины дуги в плоском сл-е для линии, задан-й ур-ем 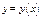равен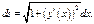

Диф-ал длины дуги в пространственном случае для линии, заданной ур-ми 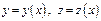равен

При парам-м задании линии 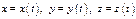диф-ал длины дуги в плоском случае равен 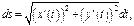а в пространственном случае -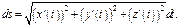

Определение. Криволинейным интегралом 1-го рода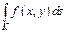 от ф-и 2х переем-х 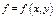(заданной в некоторой связной обл-ти), взятым по отрезку плоской кривой (этот отрезок находится в той же обл-ти и наз-ся путем интегр-я), заданной своим ур-ем, наз-ся число, получаемое следующим образом:

Отрезок 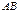разбив-ся на 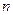элемент-х отрезков произв-но выбран-ми точками 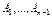, идущими от нач-а отрезка 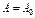до его конца .

Внутри (или на границе) каждого элем-го отрезка 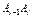выбирается одна произв--ая точка 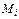с корд-ми

Знач-я ф-ции в этих выбр-х точках умножаются на длины отрезков 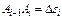(эти длины считаются полож-ми).

Все полученные 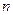произведений 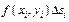складываются.

Вычисляется предел суммы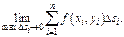

Если этот предел сущ-ет и не зависит от выбора точек то он наз-ся криволинейным интегралом 1-го род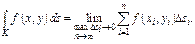а (А)

Аналогично опред-ся криволинейный интеграл 1-го рода для ф-ции 3х переем-х 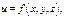взятый по отрезку пространств-й кривой 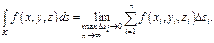(Б)