Формула Грина. Независимость кривол-го интеграла второго рода от пути. Восстановление ф-и неск-х переем-х по известному диф-лу.
Теорема. Если ф-и  и
и 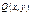 непрерывны вместе со своими производными в замкнутой области
непрерывны вместе со своими производными в замкнутой области 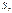 ограниченной контуром
ограниченной контуром 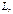 то
то 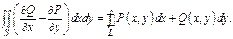
|
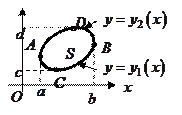
Это означает, что величина работы сил-го поля не зав-т от пути, а только от нач-й и конечной точек.
Лемма. Для того чтобы кривол-й интеграл 2-го не зависел от пути интегр-ия, необходимо и достаточно, чтобы этот интеграл, взятый по любому замкнутому контуру, был равен 0.
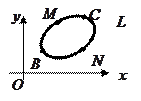
Необходимость: Пусть 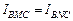 . Тогда
. Тогда 
Достаточность: Пусть 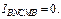 Тогда
Тогда 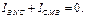 След-но
След-но 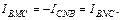
Теорема. Пусть ф-и 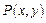 и
и 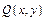 непрерывны вместе со своими производными в замкнутой области
непрерывны вместе со своими производными в замкнутой области 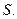 Тогда, для того чтобы кривол-й интеграл 2-го рода
Тогда, для того чтобы кривол-й интеграл 2-го рода 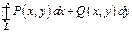 не зависел от линии интегрирования, лежащей в
не зависел от линии интегрирования, лежащей в  необходимо и достаточно, чтобы
необходимо и достаточно, чтобы 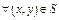 выполнялось равенство
выполнялось равенство 
Достаточность: Пусть  Тогда
Тогда 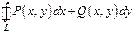

Утверждения. 1) Кривол-й интеграл 2-го рода 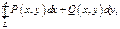 взятый по любому замкн-му контуру, целиком лежащим в
взятый по любому замкн-му контуру, целиком лежащим в 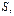 равен 0.
равен 0.
2) Кривол-й интеграл 2-го рода 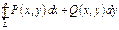 не зависит от линии интегр-ия, соединяющих две данные точки.
не зависит от линии интегр-ия, соединяющих две данные точки.
3) Во всех точках области 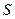

Эти утверждения эквивалентны!
Пример. 1) 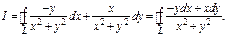 Пусть замкнутый контур
Пусть замкнутый контур  не содержит начало коорд-т.
не содержит начало коорд-т. 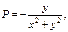
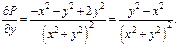
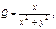
 Следов-но
Следов-но 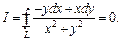
2) Рассмотрим тот же кривол-й интеграл по замкнутому контуру, содержащему начало коорд-т. Например, 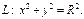 В точке
В точке 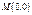 ф-и
ф-и 
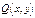 и их производные не сущ-ют. Введем параметр
и их производные не сущ-ют. Введем параметр  Тогда
Тогда 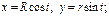
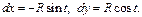

 2014-02-02
2014-02-02 342
342









