Физ-е задачи, приводящие к ДУ. ДУ первого порядка. Задача Коши. Теор-а сущ-ния и единственности реш-я задачи Коши. Основные классы ур-й, интегрируемые в квадратурах.
Связь м-у кривол-ми интегралами 1 и 2 рода.
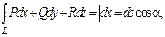
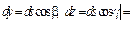
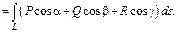
Простейшие ДУ:  или
или 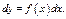 Реш-е
Реш-е 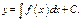
Более сложные ДУ: 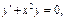
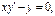
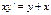 и т.д. или
и т.д. или 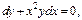
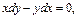
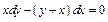 и т.д.
и т.д.
Определение. ДУ 1-го порядка наз-ся ур-ие, связывающее незав-ую переем-ю 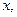 ф-ю
ф-ю  и ее произв-ю
и ее произв-ю 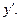
Будем рассматривать ур-я ф-ции одной перем-й.
Общий вид диф-го ур-я 1-го порядка 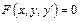 или
или 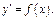
Определение. Реш-м ДУ наз-ся ф-я, кот-я при подстановке ее вместе с производной в это ур-ие, превращает его в тождество.
Примеры: 1) 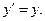 Реш-е
Реш-е 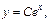 где
где 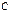 - произвольная постоянная.
- произвольная постоянная.
2) 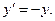 Реш-е
Реш-е 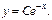
ДУ 1-го порядка 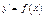 имеет бесчисленное мн-тво реш-й, которые обычно опред-ся формулой
имеет бесчисленное мн-тво реш-й, которые обычно опред-ся формулой 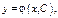 содержащей одну произв-ю постоянную. Такое множ-во решений наз-т общим реш-м ДУ. Придавая
содержащей одну произв-ю постоянную. Такое множ-во решений наз-т общим реш-м ДУ. Придавая 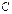 определенные (допустимые) знач-я, получим частное реш-е.
определенные (допустимые) знач-я, получим частное реш-е.
При реш-и конкретных задач нас будет интересовать частное реш-е, определяемое нач-ми усл-ми. Обычно нач-ые усл-я задаются парой знач-й 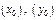 или
или 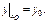
Задача отыскания частного реш-я по нач-му усл-ю наз-ся задачей Коши.
Пусть дано ДУ  и нач-е усл-е
и нач-е усл-е 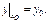 Если ф-я
Если ф-я 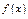 и ее частная производная
и ее частная производная 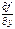 непрерывны в открытой области, содержащей точку
непрерывны в открытой области, содержащей точку 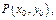 то в достаточно малом интервале
то в достаточно малом интервале 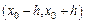 это ур-е имеет единств-е реш-е
это ур-е имеет единств-е реш-е 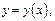 удовлетворяющее заданному нач-му усл-ю
удовлетворяющее заданному нач-му усл-ю 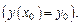
Без доказательства.
График частного реш-я ДУ наз-ся интегр-й кривой. Общее реш-е – семейство интегр-х кривых.
 Чтобы отыскать частное реш-е, нужно в общее реш-е
Чтобы отыскать частное реш-е, нужно в общее реш-е  подставить
подставить 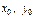 и разрешить ур-е относ-но
и разрешить ур-е относ-но 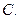
Примеры: 1) ДУ 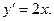 Общее реш-е
Общее реш-е 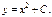
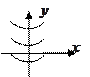 Нач-ое усл-е
Нач-ое усл-е  Подставим нач-е усл-е в общее реш-е ДУ я. Получим алгебраическое ур-ие для опред-я произв-ой постоянной
Подставим нач-е усл-е в общее реш-е ДУ я. Получим алгебраическое ур-ие для опред-я произв-ой постоянной 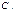
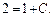 Следов-но
Следов-но 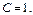 Частным реш-ем ДУ, удовлетворяющим нач-м усл-м будет
Частным реш-ем ДУ, удовлетворяющим нач-м усл-м будет 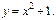
2) ДУ 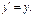 Общее решение
Общее решение 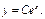
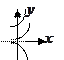
Нач-ое усл-е 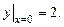 Подставим нач-е усл-е в общее реш-е ДУ. Получим
Подставим нач-е усл-е в общее реш-е ДУ. Получим 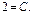 Частным реш-м ДУ, удовлетворяющим нач-м усл-м будет
Частным реш-м ДУ, удовлетворяющим нач-м усл-м будет 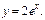
Общее реш-е ДУ не обязательно должно быть получено в явном виде. 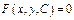 также является реш-м ДУ.
также является реш-м ДУ.
ДУ с разделяющимися переем-ми.
Рассмотрим ДУ 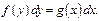 Проинтегрировав, получим
Проинтегрировав, получим 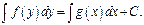 Если
Если 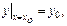 то
то 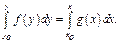
Пример: 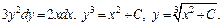
Определение. ДУ, в кот- переем-е можно разделить посредством умнож-я или дел-я обеих частей ур-я на одно и то же выражение, наз-ся ДУ с раздел-ся переем-ми. 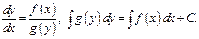
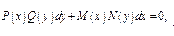
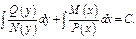
Вним-е! Может произойти потеря част-го реш-я.
 2014-02-02
2014-02-02 402
402








