ДУ высших порядков. Задача Коши. Ур-я, допускающие понижение порядка.
Определение. Ур-я вида 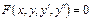 наз-ся ДУ 2-го порядка.
наз-ся ДУ 2-го порядка.
ДУ, разрешенное относительно 2-й производной  имеет вид
имеет вид 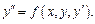
Пример. 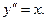 Последовательно интегрируя, получим
Последовательно интегрируя, получим 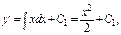
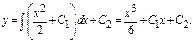
Лемма. ДУ 2-го порядка 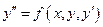 обычно имеет бесчисленное множество реш-й, определяемых формулой
обычно имеет бесчисленное множество реш-й, определяемых формулой 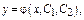 содержащей две произвольные постоянные. Это множество реш-й наз-ся общим решением.
содержащей две произвольные постоянные. Это множество реш-й наз-ся общим решением.
Частные решения ДУ определяются из нач-х усл-й 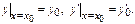
Пример. 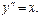
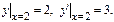

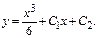
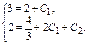
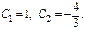
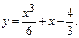
Геометр-й смысл нач-х усл-й: Помимо точки 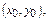 задаем угловой коэф-т касс-й.
задаем угловой коэф-т касс-й.
Если ф-я 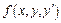 и ее производные
и ее производные 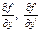 непрерывны в окрестности знач-й
непрерывны в окрестности знач-й 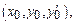 то ДУ
то ДУ 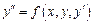 в достаточно малом интервале
в достаточно малом интервале 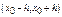 имеет единств-е реш-е
имеет единств-е реш-е 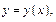 удовлетворяющее заданным нач-м усл-м
удовлетворяющее заданным нач-м усл-м 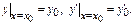
Без доказательства.
Из теоремы следует, что ур-е 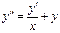 при заданных нач-х усл-х
при заданных нач-х усл-х 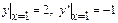 имеет единственное реш-е. Если задать нач-е усл-я при
имеет единственное реш-е. Если задать нач-е усл-я при 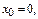 то теорема о сущ-нии дать ответ не может, т.к. при
то теорема о сущ-нии дать ответ не может, т.к. при 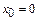 правая часть имеет особенность.
правая часть имеет особенность.
Для ДУ 2-го порядка часто задают граничные условия (краевые условия)  (сопромат (изгиб балки), математическая физика и т.д.). В этом случае может быть одно реш-е, может реш-е не сущ-ть и может быть бесконечное мн-во реш-й. Это коренное отличие задания граничных условий от задания нач-х усл-й.
(сопромат (изгиб балки), математическая физика и т.д.). В этом случае может быть одно реш-е, может реш-е не сущ-ть и может быть бесконечное мн-во реш-й. Это коренное отличие задания граничных условий от задания нач-х усл-й.
Пример. 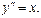
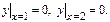
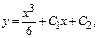
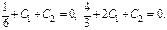
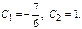
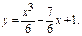
 2014-02-02
2014-02-02 417
417








