Числовые ряды. Сходимость и сумма ряда. Необходимое усл-е сход-ти. Действия с рядами. Достаточные признаки сход-ти знакополож-х рядов

Пусть дана бесконечная послед-ть .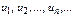

Определение. Выраж-е 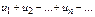наз-ся рядом, а числа 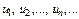- членами ряда.

Краткая запись 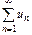. 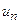- общий член ряда.

Ряд считается заданным, если задана ф-я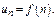

Примеры 1) .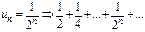

2) .

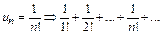Иногда ряд задают рекуррентной формулой.

Пример. 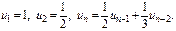Тогда 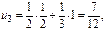и т.д.

Пусть дан ряд 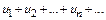. Обозначим частичной суммой ряда. Образуем последов-сть частичных сумм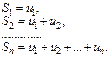

Определение. Если сущ-ет предел последов-ти 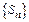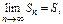то ряд сходящийся и 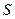- его сумма. Если послед-ть 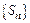не стремится к пределу, то ряд расходящийся.

Последнее имеет место в двух случаях: 1) 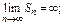2) не существует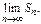

Примеры: 1)

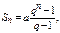
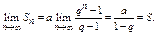
2)

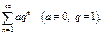
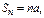
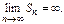
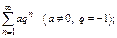
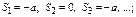
3) 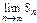не сущ-ет.