Рассмотрим ряд 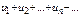 такой, что
такой, что 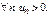
Лемма. Если частичные суммы ряда с полож-ми членами ограничены сверху 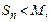 то ряд сходится.
то ряд сходится.
Док-во. 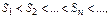 т.к.
т.к.  Если послед-ть монотонно возрастает и ограничена сверху, то по признаку сходимости Вейерштрасса она имеет предел
Если послед-ть монотонно возрастает и ограничена сверху, то по признаку сходимости Вейерштрасса она имеет предел 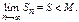
Если ряд сходится, то 
Если ряд с полож-ми членами расходится, то 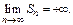
Признак сравнения. Пусть даны два ряда с полож-ми членами 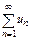 (1),
(1), 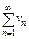 (2)
(2)  и
и 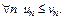 (*)
(*)
Тогда:
1) если сходится ряд (2), то сходится ряд(1);
2) если расходится ряд (1), то расходится ряд(2).
Док-во. 1) 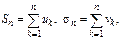
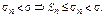 В силу леммы ряд (1) сходится.
В силу леммы ряд (1) сходится.
2) 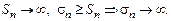
Признак справедлив, если усл-е (*) выполняется с какого-либо номера 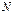 в силу 3-го св-ва сходящихся рядов.
в силу 3-го св-ва сходящихся рядов.
Пример 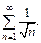 Сравним с расходящимся рядом
Сравним с расходящимся рядом 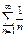 .
. 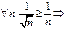 исходный ряд расходится.
исходный ряд расходится.
Предельный признак сравнения. Если 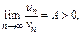 то ряды (1) и (2) сходятся или расходятся одновременно.
то ряды (1) и (2) сходятся или расходятся одновременно.
Док-во. 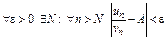 или
или 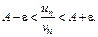 Пусть ряд (2) сходится. Тогда по свойству 1 сходящихся рядов сходится ряд
Пусть ряд (2) сходится. Тогда по свойству 1 сходящихся рядов сходится ряд 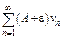 и т.к.
и т.к. 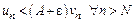 следовательно ряд (1) сходится. Если ряд (2) расходится, то в силу
следовательно ряд (1) сходится. Если ряд (2) расходится, то в силу 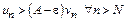 ряд (1) расходится.
ряд (1) расходится.
Пример. 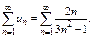 Сравним с расходящимся рядом
Сравним с расходящимся рядом 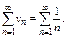
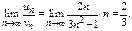 Исходный ряд расходится.
Исходный ряд расходится.
 2014-02-02
2014-02-02 613
613








