Для кратных корней реш-е усложняется. Если для одного ур-я можно сразу написать структуру общего реш-я, то здесь иначе. Покажем на примерах.
Пример 1. 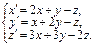
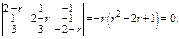
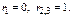
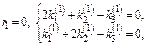
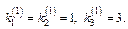
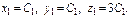
Для кратного корня  с-ма ур-й сводится к одному ур-ю
с-ма ур-й сводится к одному ур-ю 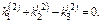 Произвольно можно задать две величины
Произвольно можно задать две величины 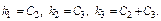 Тогда
Тогда 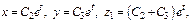 т.е.
т.е. 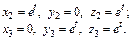
Получили фундаментальную с-му реш-й, т.к. 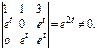
Общее реш-е 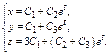
Пример 2. 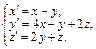
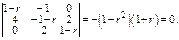
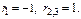
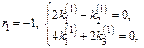
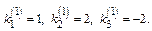
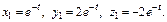
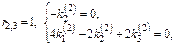
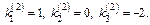

Третье реш-е таким способом получить не удастся. Будем искать реш-е в виде 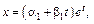
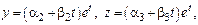
где 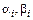 определяются методом неопределенных коэф-в. Продифференцируем
определяются методом неопределенных коэф-в. Продифференцируем 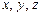 и подставим в с-му ДУ. После сокращения на
и подставим в с-му ДУ. После сокращения на 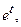 получим
получим
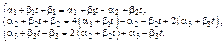
Приравнивая коэф-ты при степенях 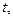 получим
получим
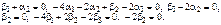
Полагая 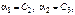 имеем
имеем 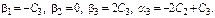 Итак
Итак
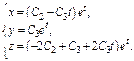
Реш-е с индексом 2 получается, если 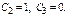 Если положить
Если положить 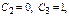 получим третье реш-е
получим третье реш-е 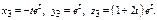
Три реш-я образуют фундаментальную с-му реш-й.
Правило. Если характеристическое ур-е с-мы ДУ имеет корень 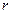 кратности
кратности 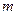 , то ему отвечает реш-е, зависящее от
, то ему отвечает реш-е, зависящее от 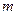 произвольных постоянных
произвольных постоянных
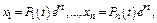 где
где 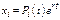 - многочлены степени не выше
- многочлены степени не выше 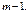
 2014-02-02
2014-02-02 410
410








