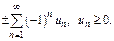
Теорема Лейбница. Если в знакочередующемся ряде 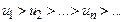 и
и 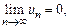 то ряд сходится. Причем
то ряд сходится. Причем 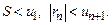
Док-во. Возьмем для определенности 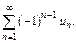 Рассмотрим последов-сть сумм
Рассмотрим последов-сть сумм 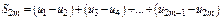 . Она возрастающая.
. Она возрастающая. 
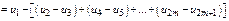 . Выражение в квадратных скобках возрастающая последовательность. Следовательно последовательность
. Выражение в квадратных скобках возрастающая последовательность. Следовательно последовательность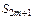 убывающая. Тогда
убывающая. Тогда 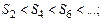
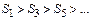 .
. 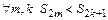 т.к. если
т.к. если 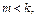 то
то 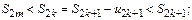 если
если 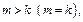 то
то 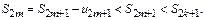 Послед-сть с четными индексами возрастает и ограничена сверху. Значит сущ-ет
Послед-сть с четными индексами возрастает и ограничена сверху. Значит сущ-ет 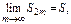 т. к.
т. к. 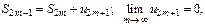 то
то 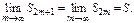 Если бы перед рядом стоял минус, то картина зеркально отразится относ-но точки
Если бы перед рядом стоял минус, то картина зеркально отразится относ-но точки 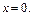 Остаток ряда
Остаток ряда 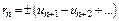 удовлетворяет усл-ям признака Лейбница. Поэтому его сумма
удовлетворяет усл-ям признака Лейбница. Поэтому его сумма 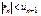
Пример. 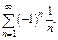 Ряд сходится по признаку Лейбница, т. к.
Ряд сходится по признаку Лейбница, т. к. 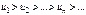 .
. 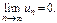 Но ряд сходится плохо, т. к.
Но ряд сходится плохо, т. к. 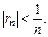
 2014-02-02
2014-02-02 358
358








