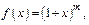Биальный ряд

где 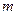- любое число.

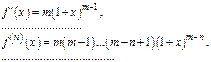
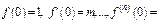
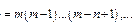
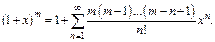
Найдем интервал сходимости. Применим признак д’Аламбера.

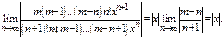Ряд сходится при 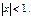Ряд расход-ся при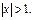

Оценим остаточный член 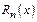для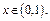

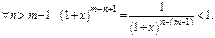
Поэтому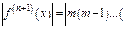

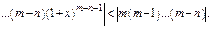
Здесь нельзя воспользоваться теоремой для оценки 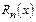, т. к. ограничение для производной зависит от 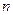. Применим нер-во, доказ-ое на прошлой лекции 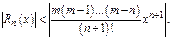Правая часть нер-ва есть 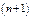-й член ряда, сходящегося при 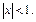След-но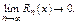

Для 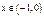док-во не приводим.

Итак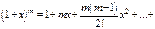

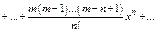
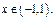
Если 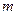- целое и больше 0, то получим формулу бинома Ньютона.

Для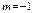

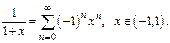
Для разных 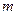могут входить в обл-ть сходимости одна или обе границы.