Разложение ф-и в ряд Маклорена.
Разложение ф-и в ряд Маклорена.
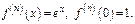 По формуле Тейлора
По формуле Тейлора 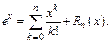
Рассмотрим интервал 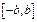 , где
, где 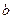 любое фиксированное число.
любое фиксированное число. 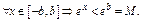 По теореме
По теореме 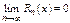 . След-но
. След-но 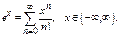 В частности для
В частности для 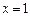
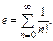
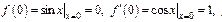
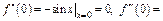
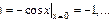
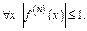
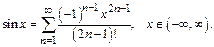
Аналог-но 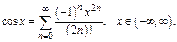
Нечетные ф-и раскладываются по нечетным степеням. Четные ф-и расклад-ся по четным степеням.
Если исследование остаточного члена 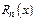 представляет затруднения (когда нельзя пользоваться доказанной теоремой) то:
представляет затруднения (когда нельзя пользоваться доказанной теоремой) то:
1) Разлагаем функцию в ряд Тейлора.
2) Находим интервал сходимости.
3) Доказываем, что 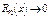 для всякого
для всякого 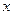 , принадлежащего интервалу сходимости.
, принадлежащего интервалу сходимости.
Обычно ряд Тейлора сходится к 
Обратный пример. 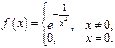
Ф-я бесконечное число раз дифференцируема 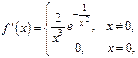 т. к.
т. к. 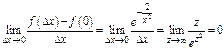 и т. д.
и т. д. 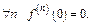
Тогда все коэф-ты ряда Тейлора равны 0. Ряд Тейлора состоит из членов равных 0 и сходится не к ф0и 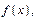 а к ф0и
а к ф0и 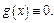
 2014-02-02
2014-02-02 549
549








