2014-02-02
330
Разложение ф-й проводится в два этапа:
1) Вычисляются производные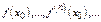 
. Составляется ряд Тейлора.
2) Находится интервал, где ряд Тейлора сходится, т. е.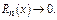 
Теорема. Если в нек-ром интервале, окруж-щем точку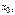 
абсолютные величины всех производных ф-и 
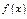огранич-ы одним и тем же числом, то ф-я 
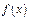в этом интервале разлаг-ся в ряд Тейлора.
Доказательство. По усл-ю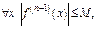 
где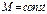 
(не зависит от 
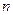). Тогда для всякого 
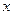, принадлежащего интервалу, 
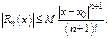Но 
Следов-но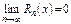 
для всякого 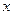, принадлеж-го интервалу. Особенно часто исп-ют разложение при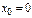 
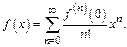Этот ряд наз-ся рядом Маклорена.
