Природа высокоэластичности на молекулярно-кинетическом уровне рассматривается в рамках статистической термодинамики. В простейших статистических теориях полимерную молекулу моделируют в виде бестелесной свободно-сочлененой цепи, отдельные звенья которой подвергаются хаотическому тепловому движению. Статистический расчет вероятности того, что для достаточно многозвенной свободно-сочлененной цепи, один из концов которой закреплен в произвольной точке, а другой находнтся в элементарном объеме dΩ, отстоящем от этой точки на растояние r, приводит к функции распределения Гаусса:
|
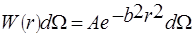
где b и A выражаются через параметры, характеризующие макромолекулу:
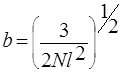 ;
; 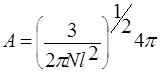
здесь N —число звеньев, l — длина звена.
Величина W(r)dΩ пропорциональна термодинамической вероятности цепи, т.е. числу возможных ее конформаций при данном растоянии между концами. Подставляя (19) в выражение Больцмана, получаем для энтропии макромолекулы:
|
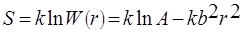
где k — постоянная Больцмана.
Поскольку при выводе функции распределения используется модель свободно-сочлененной цепи, то, очевидно, предполагается, что изменение конформации макромолекулы не сопровождается изменением внутренней энергии. Отсюда следует, что при деформации свободно-сочлененной цепи (например, при растяжении) изменение ее свободной энергии полностью обусловлено изменением ее энтропии.
Исходя из этих представлений и используя приведенные выше термодинамические соотношения, можно найти связь между силой, приложенной к макромолекуле, и се удлинением:
|
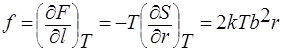
Таким образом, упругость полимерной цепи обусловлена уменьшением числа возможных конформации цепи (т.е. уменьшением энтропии) при растяжении.
Из уравнения (21) следует, что макромолекула, концы которой закреплены в определенных точках, подвергается действию силы, направленной вдоль линии, соединяющей эти концы и стремящейся их сблизить. Эта сила пропорциональна расстоянию между концами цепи и температуре. Если в стеклообразных и кристаллических полимерах модуль упругости уменьшается с повышением температуры, то в случае высокоэластических полимеров модуль упругости при повышении температуры возрастает. Это обусловлено тем, что с повышением температуры увеличивается интенсивность теплового движения звеньев полимерной цепи совершенно так же, как увеличение давления разреженного газа при нагревании обусловлено увеличением интенсивности теплового движения его молекул.
Полимерные материалы, эксплуатируемые в высокоэластическом состоянии, обычно представляют собой непрерывные сетки из сшитых друг с другом макромолекул.
Зависимость равновосного напряжения от деформации для такой сетки описывается уравнением
|
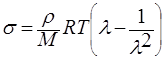
где ρ — плотность полимера; M — молекулярная масса отрезка цепи, заключенного между двумя соседними узлами; λ — отношение длины растянутого образца к его первоначальной длине.
|
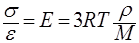
где E — равновесный модуль упругости каучука при растяжении.
Таким образом, кинетическая теория высокоэластичности описывает принципиальные особенности механического поведения полимера, находящегося в высокоэластическом состоянии.
В то же время наличие внутри- и межмолекулярных взаимодействий в реальных полимерах обусловливает конечную скорость изменения формы цепных макромолекул. Поэтому помимо зависимости равновесной деформации полимеров от приложенного напряжения следует учитывать и время действия этого напряжения.
 2014-02-02
2014-02-02 2032
2032








