Термодинамика высокоэластической деформации. Способность к развитию больших обратимых (высокоэластических) деформаций является уникальным свойством полимерных материалов. Это свойство описывают кривой зависимости деформации ε от прилагаемого напряжения σ — так называемой деформационно-прочностной кривой или кривой растяжения (рис.16).
Максимальное обратимое удлинение таких высокомолекулярных соединений, как каучуки, может достигать тысячи и более процентов. Модуль упругости каучука — отношение σ/ε в области небольших деформаций, в которой соблюдается закон Гука, составляет порядка 1 МПа (модули упругости типичных низкомолекулярных твердых тел достигают примерно 105 МПа, а их наибольшая обратимая деформация редко превышает 1 %).
|
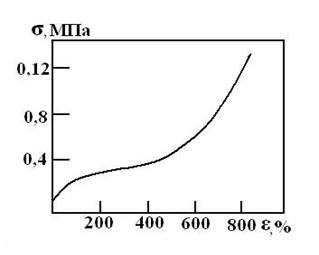| Рис.16 Кривая растяжения натурального каучука.
|
Для того чтобы понять природу высокоэластичности, необходимо прежде всего рассмотреть изменение термодинамических функций состояния полимера при его высокоэластической деформации. Из самых общих соображений можно вывести соотношения между длиной образца l, упругой силой f и температурой Т, с одной стороны, и его внутренней энергией U и энтропией S — с другой.
Согласно первому закону термодинамики изменение внутренней энергии системы
U определяется количеством тепла
dQ, подведенного к системе извне, и работой
dA, совершенной над системой. Следовательно, в обратимом процессе
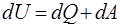(10)
Из второго закона термодинамики следует, что в обратимом процессе
Работа, затрачиваемая при растяжении образца на величину
dl, в общем случае равна
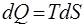
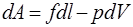
где dV —изменение объема образца при растяжении; p – внешнее давление.
Из опыта следует, что изменение объема полимера при деформации в высокоэластическом состоянии крайне незначительно и при давлении, равном примерно атмосферному, член pdV меньше, чем fdl в 103 — 104 раз. Следовательно, этим членом можно пренебречь. Учитывая последнее обстоятельство и комбинируя уравнения (1) — (3), получим:
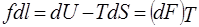
где (dF)T — изменение энергии Гельмгольца в изотермических условиях.
Отсюда:
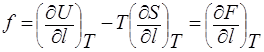
Таким образом, возникающая в образце упругая сила в общем случае связана с изменением его свободной энергии.
Пользуясь известными термодинамическими соотношениями, можно преобразовать уравнение (5). Придав ему форму, пригодную для экспериментальной оценки энергетического и энтропийного вкладов в упругую силу, возникающую в полимере при высокоэластической деформации. Для этого воспользуемся выражением полного изменения энергии Гельмгольца F:
и подставим в него уравнение
(4). Получаем:
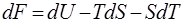
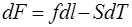
Функция F, будучи функцией состояния системы, имеет полный дифференциал:
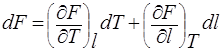
Сравнивая выражение полного дифференциала с уравнением (6), имеем:
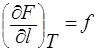и
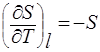
Пользуясь свойством частных производных функций, имеющей полный дифференциал, можно записать:
т.е.
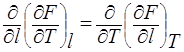
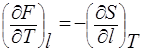
После подстановки (17) в (14) получим:
|
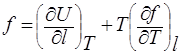
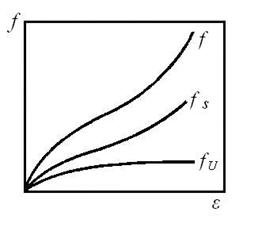Рис.17 Зависимость упругойсимы f, ее энергетической fU и энтропийной fS составляющих от степени растяжения натурального каучука при 20 С.
|
Из уравнения ( 18 ) следует, что. измеряя равновесную силу в зависимости от температуры при постоянной длине растянутого образца, можно оценить энергетическии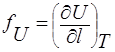 
и энтропийный 
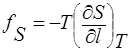вклады в упругую силу. На рис.17 приведены экспериментальные результаты, полученные для слабосшитого натурального каучука. Как видно из рис.17, основной вклад в равновесную эластическую силу вносит энтропийный член fS, в то премя как энергетический член fU весьма мал и практически не изменяется до сравнительно больших значений удлинения. Такое поведение резко отличает полимеры в высокоэластическом состоянии от низкомолекулярных твердых тел, деформация которых в первую очередь сопровождается изменением внутренней энергии. В термодинамическом аспекте деформация высокоэластических тел аналогична сжатию разреженных газов.
2014-02-02
3911
