2014-02-02
308
Пример 4
Вычислить производные логарифмических функций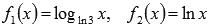 
.
Решение.
Формулу мы уже вывели, так давайте ею и воспользуемся (в первом случае основание логарифма равно натуральному логарифму трех a = ln3, во втором a = e):
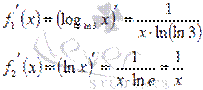
Найти производную функции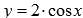 
.
Решение.
Из таблицы производных для тригонометрических функций видим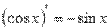 
. Воспользуемся правилом вынесения множителя за знак производной:
Достаточно часто приходится сначала упрощать вид дифференцируемой функции, чтобы воспользоваться таблицей производных и правилами нахождения производных. Следующие примеры это наглядно подтверждают.
