Домашнее Задание
Пример 11
Найти производную функции  .
.
Решение.
Функция представляет собой разность выражений 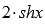 и
и 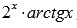 , поэтому
, поэтому
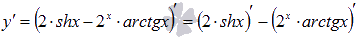
В первом выражении выносим двойку за знак производной, а ко второму выражению применяем правило дифференцирования произведения:
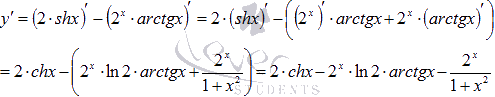
1) 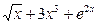
| 2) 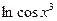
| 3) 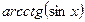
|
4) 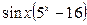
| 5) 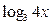
| 6) 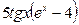
|
7) 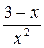
| 8) 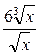
| 9) 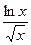
|
10) 
| 11) 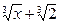
| 12) 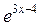
|
13) 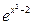
| 14) 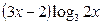
| 15) 
|
16) 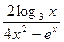
| 17) 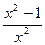
| 18) 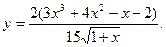
|
19) 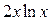
| 20) 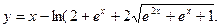
| 21) 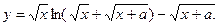
|
22) 
| 23) 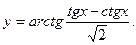
| 24) 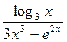
|
Лекция________. Производные высших порядков
Пусть y = f (x) является дифференцируемой функцией. Тогда производная также представляет собой функцию от x. Если она является дифференцируемой функцией, то мы можем найти вторую производную функции f, которая обозначается в виде
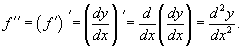
Аналогично, если f '' существует и дифференцируема, мы можем вычислить третью производную функции f:
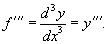
Производные более высокого порядка (если они существуют), определяются как
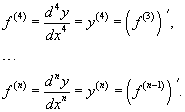
Для нахождения производных высшего порядка можно использовать следующие формулы:
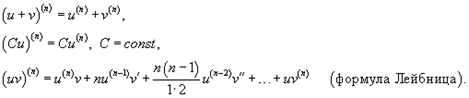
В частности, для производной второго и третьего порядка формула Лейбница принимает вид
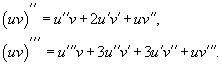
Найти y'', если 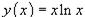 .
.
Решение.
Возьмем первую производную, дифференцируя функцию как произведение:
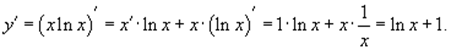
Теперь найдем производную второго порядка: 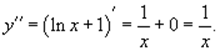
 2014-02-02
2014-02-02 481
481








