1°. 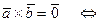
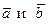 – коллинеарные векторы;
– коллинеарные векторы;
2°. 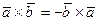 ;
;
3°. 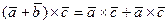 ;
;
4°. 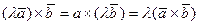 .
.
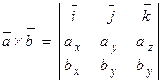 . (2.11)
. (2.11)
Основные приложения векторного произведения.
1)  Вычисление площади треугольника (параллелограмма). Из курса математики средней школы известно, что площадь треугольника равна половине произведения его сторон на синус угламеждуними, что совпадает с половиной модуля векторного произведения векторов, которые построены на сторонах треугольника. Таким образом,
Вычисление площади треугольника (параллелограмма). Из курса математики средней школы известно, что площадь треугольника равна половине произведения его сторон на синус угламеждуними, что совпадает с половиной модуля векторного произведения векторов, которые построены на сторонах треугольника. Таким образом,
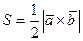 ,
,
где S площадь треугольника с вершинами в точках А, В, С, 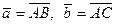 (рис. 2.9).
(рис. 2.9).
2) Вычисление высоты треугольника (параллелограмма).
Вычислим площадь треугольникадвумя способами:
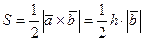 ,
,
где h – высота треугольника, опущеннаяиз вершины В (рис. 2.9). Из этого равенства получаем:
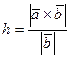 .
.
Пример. 2.1. Найти площадь треугольника с вершинами в точках А (1, 1, 1), В (1, 2, 3), С (3, 2, 1) и высоту, опущенную из вершины В на сторону АС (рис. 2.9).
Решение. Пусть 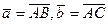 , тогда
, тогда
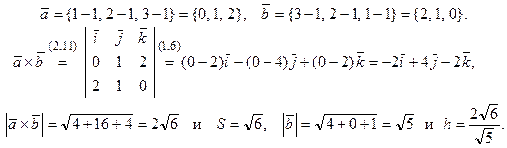
 2014-02-02
2014-02-02 910
910








