Скалярное произведение векторов и его свойства. Скалярным произведением векторов называется число, равное произведению длин этих векторов на косинус угла между ними

Скалярным произведением векторов 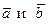называется число, равное произведению длин этих векторов на косинус угла между ними. Обозначение: 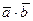или .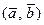

Таким образом, по определению

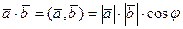, (2.7)

где 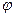угол между векторами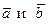. По формуле (2.1)

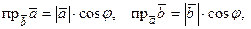
т.е.

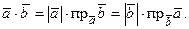(2.8)

Свойства скалярного произведения векторов (ненулевые векторы)

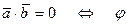. прямой угол (),

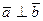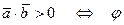острый угол,

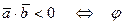тупой угол;

2^о.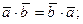

3^о.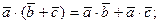

4^o.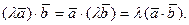

Произведение 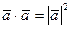называется скалярным квадратом вектора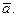

Скалярное произведение векторов равно сумме попарных произведений соответствующих координат этих векторов:

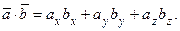(2.9)

Основные приложения скалярного произведения