Пример 3

Пример 2.

Пример 1.

.

.

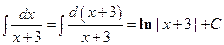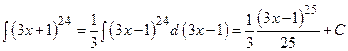
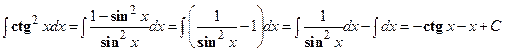1. Метод интегрирования способом подстановки (замены переменой)

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (т.е. подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся.

Пусть требуется найти интеграл 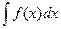. Сделаем подстановку 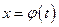, где 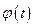- функция, имеющая непрерывную производную.

Тогда 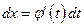и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой

.

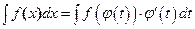Формула также называется формулой замены переменных в неопределенном интеграле. После нахождения интеграла в правой части равенства следует перейти от новой переменной интегрирования t назад к переменной х.

Иногда целесообразно подбирать подстановку в виде 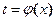, тогда 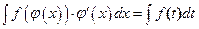, где 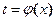. Т. е. формулу можно применять справа налево.

Функцию следует выбирать так, чтобы можно было вычислить неопределенный интеграл, стоящий в правой части равенства (2).

Приведем несколько примеров на интегрирование с помощью замены переменных.