Интегрирование тригонометрических функций

Пример 3.

Пример 2.

Требуется вычислить 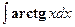. Положим 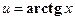, , 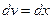тогда 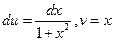. Следовательно,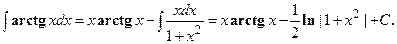

Требуется вычислить .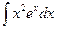

Положим 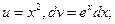тогда .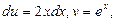

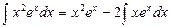Последний интеграл снова интегрируем по частям, полагая

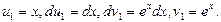Тогда

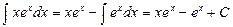. Окончательно будем иметь

.

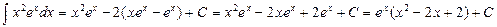Рассмотрим некоторые случаи нахождения интеграла от тригонометрических функций. Функцию с переменными 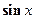, , 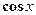над которыми выполняются рациональные действия принято обозначать 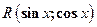, где R - знак рациональной функции.