2014-02-02
528
Неопределенный интеграл
Рассмотрим задачу: Дана функция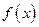 
. Требуется найти такую функцию 
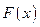, производная которой равна 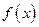, т.е. 
.
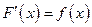Определение: Функция 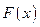называется первообразной функции 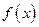на интервале 
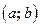, если для любого
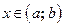выполняется равенство 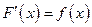или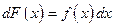 
.
Пример. Найти первообразную от функции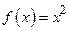 
. Из определения первообразной следует, что функция 
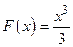является первообразной, так как 
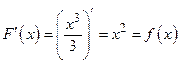. Очевидно, что первообразными будут также любые функции 
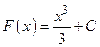, где С – постоянная, поскольку 
.
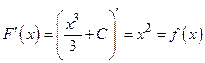Теорема. Еслифункция 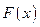является первообразной для функции 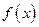на 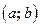, то множество всех первообразных для 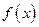задается формулой 
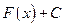, где С – постоянное число.
Функция 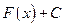является первообразной для 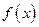. Действительно, 
.
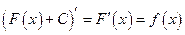Множество всех первообразных функций 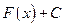для 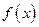называется неопределенным интеграломот функции 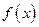и обозначается символом 
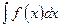. Таким образом, по определению 
.
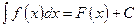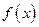называется подынтегральной функцией, 
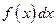- подынтегральным выражением, х – переменной интегрирования, 
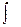- знаком неопределенного интеграла.
Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.
Геометрически неопределенный интеграл представляет семейство «параллельных» кривых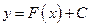 
. График каждой первообразной (кривой) называется интегральной кривой.
Для всякой ли функции 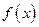существуют первообразные (а значит, и неопределенный интеграл)? Оказывается, что не для всякой. Если функция 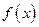непрерывна на 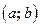,то для этой функции существует первообразная а следовательно, и неопределенный интеграл.
Нахождение первообразной для данной функции f(x) называется интегрированием функции f(x).
