2014-02-02
4781
Пусть функция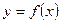 
непрерывна на отрезке 
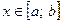. Тогда объём тела, полученного вращением вокруг оси 
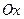криволинейной трапеции, ограниченной сверху графиком функции 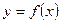, снизу (Рис. 10), определяется формулой:
. (11)
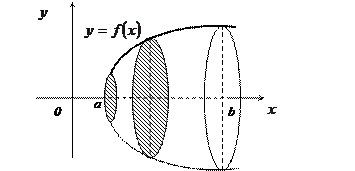
Рис. 10
Пример 15. Вычислить объем тела, полученного вращением вокруг оси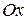 
криволинейной трапеции, ограниченной гиперболой 
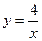, прямыми 
, 
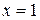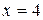и осью .
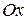Решение: Сделаем чертеж (Рис. 11, 12).
Из условия задачи следует, что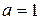 
, 
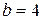. По формуле (9) получаем
.
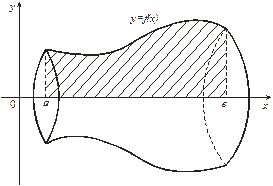
Рис. 11
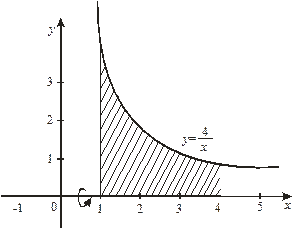
Рис. 11
Объем тела, полученного вращением вокруг оси Оу криволинейной трапеции, ограниченной прямым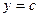и 
и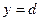 
, осью Оу и графиком непрерывной на отрезке 
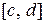функции 
.
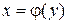Если криволинейная трапеция ограниченна графиком непрерывной функции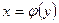 
и прямыми 
, , 
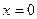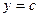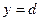
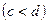, то объём тела, образованного вращением этой трапеции вокруг оси 
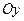, равен:
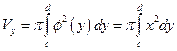. (12)
Рис. 12
Пример 16. Вычислить объем тела, полученного вращением вокруг оси Оу криволинейной трапеции, ограниченной линиями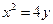 
, 
, 
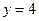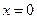(Рис. 13).
Решение: В соответствии с условием задачи находим пределы интегрирования: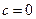 
, 
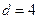. По формуле (10) получаем:
.
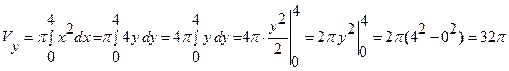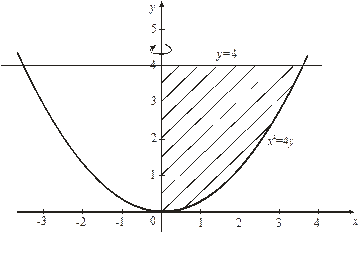
Рис. 13
