Пусть кривая 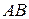 , заданная уравнением
, заданная уравнением 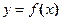 , где
, где 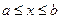 , лежит в плоскости
, лежит в плоскости  (Рис. 14).
(Рис. 14).
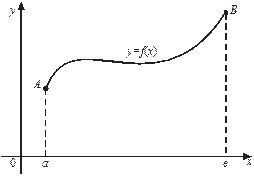
Рис. 14
Определение. Под длиной дуги 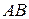 понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной стремится к бесконечности, а длина наибольшего звена стремится к нулю.
понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной стремится к бесконечности, а длина наибольшего звена стремится к нулю.
1. Для кривой, заданной уравнением 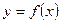 ,
, 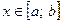
Если функция 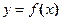 и ее производная
и ее производная 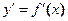 непрерывны на отрезке
непрерывны на отрезке 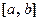 , то длина дуги кривой
, то длина дуги кривой 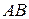 вычисляется по формуле
вычисляется по формуле
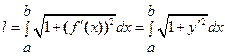 . (13)
. (13)
Пример 17. Вычислить длину дуги кривой 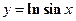 , заключенной между точками, для которых
, заключенной между точками, для которых 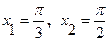 .
.
Решение: Из условия задачи имеем  . По формуле (13) получаем:
. По формуле (13) получаем:
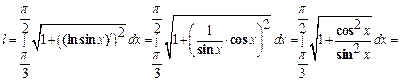
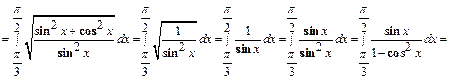
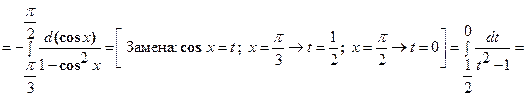
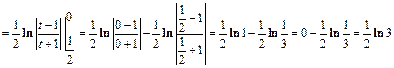 .
.
2. Для кривой, заданной параметрически уравнениями 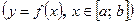
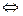
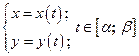 .
.
Если уравнение кривой АВ задано в параметрической форме 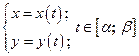
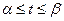 , где
, где 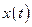 и
и 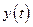 - непрерывные функции с непрерывными производными и
- непрерывные функции с непрерывными производными и 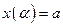 ,
, 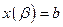 , то длина l кривой АВ находится по формуле:
, то длина l кривой АВ находится по формуле:
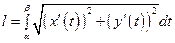 . (14)
. (14)
Пример 18. Вычислить длину дуги кривой:
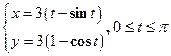 ,
,
В данном случае кривая задана параметрически, поэтому для вычисления её длины мы применим формулу (14).
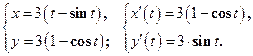
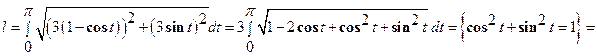
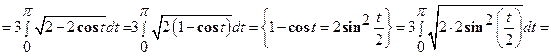
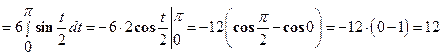 ;
;
 2014-02-02
2014-02-02 6538
6538
