Интегрирования по частям в определенном интеграле
Теорема 4. Если функции 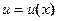 и
и 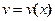 имеют непрерывные производные на отрезке
имеют непрерывные производные на отрезке 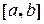 . Тогда имеет место следующая формула интегрирования по частям:
. Тогда имеет место следующая формула интегрирования по частям:
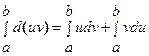 .(5)
.(5)
Так как 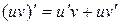 , то функция
, то функция  является первообразной для функции
является первообразной для функции 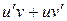 . Тогда по формуле Ньютона–Лейбница получаем
. Тогда по формуле Ньютона–Лейбница получаем
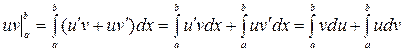 , откуда
, откуда
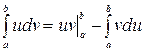 . (6)
. (6)
Формула (6) называется формулой интегрирования по частям в определенном интеграле.
Пример 8. Вычислить 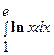 .
.
Решение: Положим 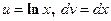 , отсюда
, отсюда 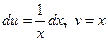 .
.
По формуле (4) находим 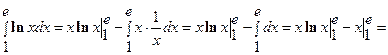
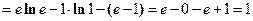 .
.
Пример 9. Вычислить 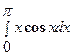 .
.
Решение: Пусть 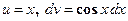 , тогда
, тогда 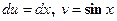 . Применяя формулу интегрирования по частям, получаем
. Применяя формулу интегрирования по частям, получаем

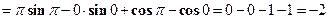 .
.
Пример 10. Вычислить 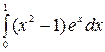 .
.
Решение: Полагая 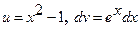 , определяем
, определяем 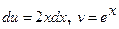 .
.
Следовательно, 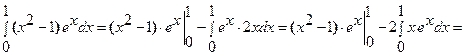
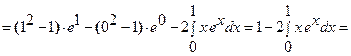 [к полученному интегралу снова применяем формулу интегрирования по частям:
[к полученному интегралу снова применяем формулу интегрирования по частям: 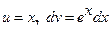 ; следовательно:
; следовательно: 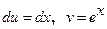 ] =
] = 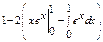 =
= 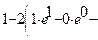
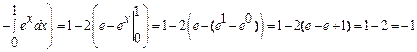 .
.
 2014-02-02
2014-02-02 2368
2368
