При построении графика функции сначала проводят исследование функции. При этом придерживаются следующего (примерного) плана:
1) находят область определения функции;
2) указывают точки пересечения с осями координат;
3) определяют точки разрыва и устанавливают тип разрыва;
4) с помощью первой производной устанавливают интервалы монотонности (т.е. интервалы возрастания и убывания) функции и находят точки экстремума и значения функции в этих точках;
5) с помощью второй производной устанавливают интервалы выпуклости, вогнутости и находят точки перегиба;
6) находят асимптоты функции.
Затем по этим данным строят график функции.
Пример 3. Построить график функции 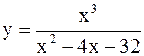 .
.
Решение. 1) Нулями знаменателя являются 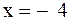 и
и 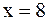 . Следовательно, областью определения функции является множество
. Следовательно, областью определения функции является множество 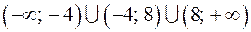 .
.
2) Найдём точки пересечения с осями координат:
а) c осью 0x. Найдём нули функции: 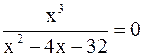 лишь при x = 0; значит, график функции пересекает ось 0x (или касается оси 0x) в точке O(0; 0) – начале координат;
лишь при x = 0; значит, график функции пересекает ось 0x (или касается оси 0x) в точке O(0; 0) – начале координат;
б) c осью 0y. Для нахождения общей точки графика функции и оси 0y следует найти f(0): f(0) = 0. Поэтому график пересекает ось 0y в точке O(0; 0).
3) Наша функция представляет собой отношение двух многочленов, поэтому она непрерывна всюду, за исключением нулей знаменателя: 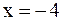 и x = 8. Найдём левые и правые пределы в этих точках.
и x = 8. Найдём левые и правые пределы в этих точках.
Для точки 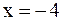 :
:

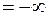 ;
;
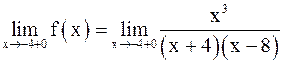
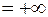 .
.
Отсюда делаем вывод, что 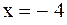 является точкой разрыва второго рода.
является точкой разрыва второго рода.
Для точки x = 8:
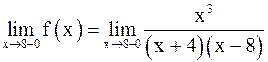
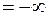 ;
;
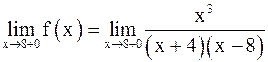
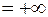 .
.
Поэтому x = 8 также является точкой разрыва второго рода.
4) Имеем
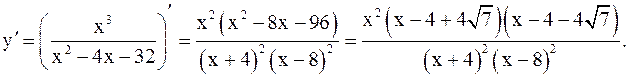
Критическими точками функции являются её стационарные точки 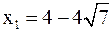 ,
, 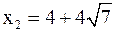 ,
, 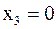 . Знак
. Знак 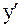 совпадает со знаком выражения
совпадает со знаком выражения 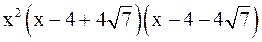 .
.
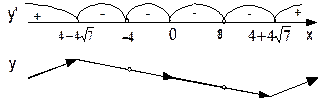
Видно, что функция возрастает на промежутках 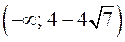 и
и 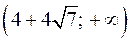 и убывает на промежутках
и убывает на промежутках 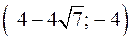 ,
, 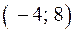 ,
, 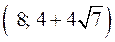 . Следовательно, точка
. Следовательно, точка 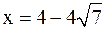 является точкой максимума (на рисунке ей соответствует «горка»), точка
является точкой максимума (на рисунке ей соответствует «горка»), точка 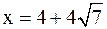 – точкой минимума (ей соответствует «впадина»). Стационарная точка
– точкой минимума (ей соответствует «впадина»). Стационарная точка 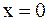 не является точкой экстремума. Найдём значение функции в точках экстремума: f(
не является точкой экстремума. Найдём значение функции в точках экстремума: f(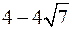 )» –7,57; f(
)» –7,57; f(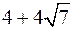 )» 25,35.
)» 25,35.
5) 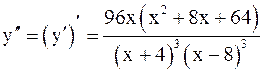 .
.
Трёхчлен 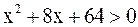 при всех x (его дискриминант меньше 0). Поэтому знак
при всех x (его дискриминант меньше 0). Поэтому знак  совпадает со знаком дроби
совпадает со знаком дроби 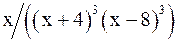 .
.
Составим схему. Видно, что функция выпукла в интервалах (–¥; –4)

и (0; 8) и вогнута в интервалах (–4; 0) и (8; +¥). При переходе через точки – 4, 8, 0  меняет свой знак. Поэтому точка x = 0 является точкой перегиба (в точках x = - 4, x = 8 функция не определена).
меняет свой знак. Поэтому точка x = 0 является точкой перегиба (в точках x = - 4, x = 8 функция не определена).
6) Так как 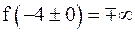 ,
, 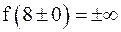 , то прямые
, то прямые  и
и
x = 8 являются вертикальными асимптотами. Найдём наклонные асимптоты при x ® –¥ и при x ® +¥. Уравнения этих асимптот будем искать в виде y = kx + b:
а) x ® –¥.
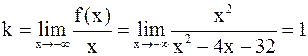 ,
,
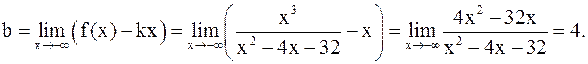
Таким образом, прямая y = x + 4 является асимптотой при x ® –¥;
б) при x ® +¥ получим тот же результат: прямая y = x + 4 является асимптотой.
Основываясь на полученных данных, построим график функции.

 2014-02-02
2014-02-02 885
885







