2014-02-02
7180
d =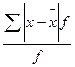 
Пример: имеются следующие данные о возрасте работников предприятия
| Группы рабочих по возрасту | Число рабочих | Середина интервала |
| ДО 20 | 17,5 | |
| 20-25 | 22,5 | |
| 25-30 | 27,5 | |
| 30-35 | 32,5 | |
| 35-40 | 37,5 | |
| 40 и старше | 42,5 | |
| ИТОГО |
Требуется определить среднее линейное отклонение возраста рабочих.
1. Рассчитаем средний возраст рабочих: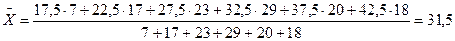 
2. Рассчитаем среднее линейное отклонение:
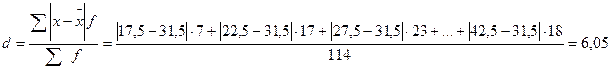
3. Среднее квадратическое отклонение рассчитывается двумя способами:
3.1. Среднее квадратическое отклонение простое: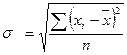 
.
Пример:
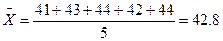
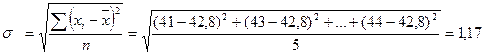
3.2. Среднее квадратическое отклонение взвешенное: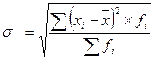 
Пример:
| Группы рабочих по возрасту | Число рабочих | Середина интервала |
| ДО 20 | 17,5 | |
| 20-25 | 22,5 | |
| 25-30 | 27,5 | |
| 30-35 | 32,5 | |
| 35-40 | 37,5 | |
| 40 и старше | 42,5 | |
| ИТОГО |
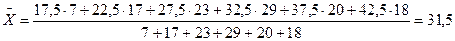
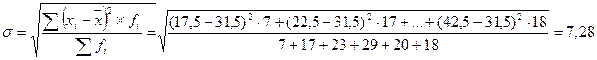
4.Дисперсия (средний квадрат отклонений) рассчитывается как простая и взвешенная, а также способом моментов:
4.1. Дисперсия простая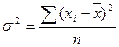 
4.2. Дисперсия взвешенная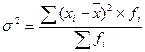 
4.3. Если варианты признака представлены не большими числами расчет дисперсии удобнее вести способом моментов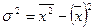 
. Способом моментов дисперсия также рассчитывается как простая: 
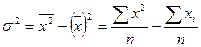; или как взвешенная: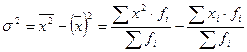 
|
|
|
Дисперсия и среднее квадратическое отклонение взаимосвязаны: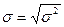 
5. Коэффициент вариации определяется как отношение среднего квадратического отклонения к средней величине признака, выраженное в процентах: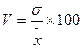
.
Он характеризует количественную однородность статистической совокупности. Если данный коэффициент < 10%, вариация признака в исследуемой совокупности является незначительной, и для формирования обобщающей характеристики признака по всем единицам данной совокупности можно использовать среднее значение.
Если коэффициент вариации 10%< V<30%, говорят об умеренной вариации признака. В такой ситуации средняя величина может быть использована для обобщающей характеристики признака в данной совокупности, НО с дополнительным анализом вариации.
Если коэффициент вариации 30%< V, вариация признака существенна (совокупность неоднородна по данному признаку). Следовательно, средняя величина не может использоваться для формирования обобщающей характеристики изучаемого признака в данной совокупности.
