Пусть есть СВ 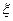 для которой плотность распределения задаётся формулой:
для которой плотность распределения задаётся формулой:
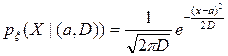 , где
, где 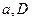 - неизвестные параметры,
- неизвестные параметры, 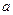 - математическое ожидание,
- математическое ожидание, 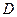 - дисперсия. Полученная выборка
- дисперсия. Полученная выборка 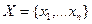 является реализованная СВ
является реализованная СВ 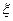 .
.
Найдём оценки 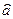 и
и 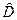 неизвестных параметров:
неизвестных параметров:
Запишем функцию правдоподобия:
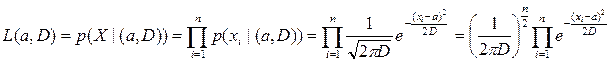 ,
,
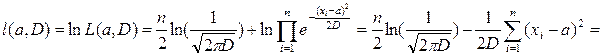
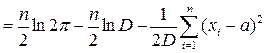 ,
, 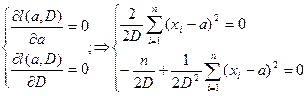 .
.
Получим:
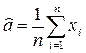 ,
, 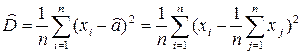 .
.
Свойства оценок нормального распределения:
1) 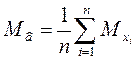 , т.к. математическое ожидание случайной величины равно
, т.к. математическое ожидание случайной величины равно 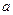 :
: 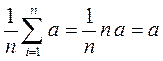 .
.
2) 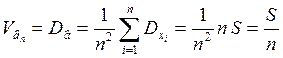 , где
, где 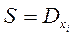 .
.
Исследуем поведение оценки:
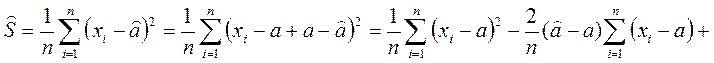
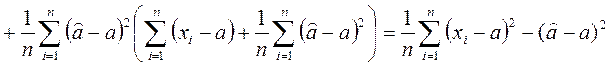 ,
,
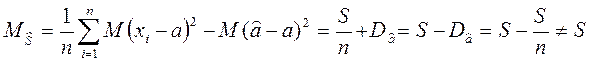 ,
,
Упражнение: 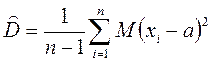 - несмещённая оценка параметра
- несмещённая оценка параметра 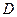 .
.
 2014-02-02
2014-02-02 745
745








