Если известен закон распределения оценки или её дисперсия, то можно указать приделы в которых с большой вероятностью находятся неизвестные значения параметра.
Пусть имеется выборка 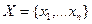 . Предположим, что выборочные значения распределены по закону:
. Предположим, что выборочные значения распределены по закону: 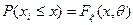 с точностью до
с точностью до 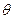 .
.
Предположим, что мы нашли функцию: 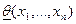 и
и 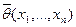 , причём
, причём 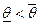 ,
, 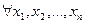 и
и 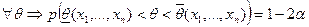 . Величина
. Величина 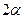 называется доверительным уровням. Обычно
называется доверительным уровням. Обычно 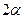 берётся очень маленьким: 0.05, 0.01…
берётся очень маленьким: 0.05, 0.01…
Вероятность того, что 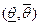 покроет неизвестный параметр
покроет неизвестный параметр 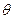 не зависит от
не зависит от 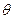 . В этом случаи интервал
. В этом случаи интервал 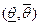 - доверительный интервал для неизвестного параметра соответствующей доверительной вероятности
- доверительный интервал для неизвестного параметра соответствующей доверительной вероятности 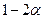 .
.
Пример:
Пусть имеется выборка 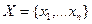 . Предположим, выборка распределена по нормальному закону:
. Предположим, выборка распределена по нормальному закону: 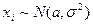 , где
, где 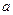 - неизвестно, а
- неизвестно, а 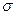 - известно.
- известно.
Найдём доверительный интервал для параметра 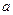 . Известно, что
. Известно, что 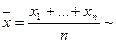 (по центральной предельной теореме)
(по центральной предельной теореме) 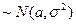 , тогда величина
, тогда величина 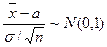 распределена по закону
распределена по закону 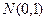 . Доверительный интервал будем строить используя следующее соотношение:
. Доверительный интервал будем строить используя следующее соотношение:
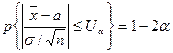 , где
, где 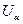 -находится путём решения уравнения:
-находится путём решения уравнения: 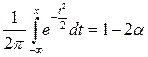 (по заданному уровню
(по заданному уровню 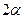 ). Окончательно имеем:
). Окончательно имеем: 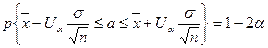 . Доверительный интервал имеет вид:
. Доверительный интервал имеет вид: 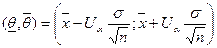 .
.
 2014-02-02
2014-02-02 336
336








