Пусть имеется W-пространство неизвестных параметров 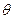 входящих в плотность распределения
входящих в плотность распределения 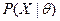 . Пространство
. Пространство 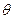 разбито на k областей
разбито на k областей 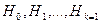 . По результатам эксперимента надо ответить на следующий вопрос:
. По результатам эксперимента надо ответить на следующий вопрос:
Какой из областей принадлежит неизвестный параметр 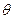 .
.
Определение: Предположение о том, что неизвестный параметр 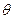 принадлежит, какой-либо области
принадлежит, какой-либо области 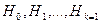 называется альтернативой.
называется альтернативой.
Определение: Совокупность k альтернатив называется k-альтернативной гипотезой.
Замечание: В литературе альтернативой так же называется гипотеза.
Определение: Если область соответствующая какой-либо альтернативе состоит из одной точки, то это альтернатива называется простой, в противном случае сложной.
Определение: Если все альтернативы простые, то гипотеза называется простой.
Определение: Если хотя бы одна альтернатива является сложной, то гипотеза называется сложной.
Обозначим решение, что имеет место i-я альтернатива, 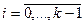 через
через 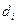 . Тогда построим правило, такое, что для любой
. Тогда построим правило, такое, что для любой 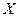 (выборки), ставим в соответствие одно из решений
(выборки), ставим в соответствие одно из решений 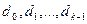 .
.
Решающие правила делятся на:
- Рандомизированные;
- Нерандомизированные.
Рандомизированные:
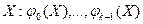 , где
, где 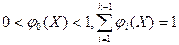 ,
, 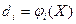 (решение выносится случайным образом).
(решение выносится случайным образом).
Нерандомизированные:
 Выборка
Выборка 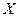 разбивается на k областей и попадание точки в i-ю область приводит к вынесению решения
разбивается на k областей и попадание точки в i-ю область приводит к вынесению решения 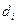 .
.
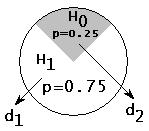
Мы будем рассматривать рандомизированные решающие правила и 2-альтернативные гипотезы:
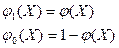 .
.
 2014-02-02
2014-02-02 392
392








