Суть МНК заключается в следующем: 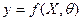 , где
, где 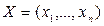 . Заменяя значения
. Заменяя значения 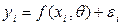 , где
, где 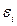 - ошибка измерений.
- ошибка измерений.
Предположим что 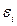 - независимые нормально распределённые случайные велечины.
- независимые нормально распределённые случайные велечины.
Плотность 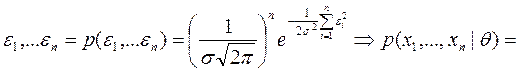
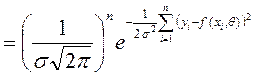 , при
, при 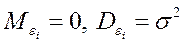 .
.
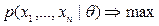
Данная задача равносильна: 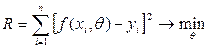 .
.
Метод наименьших квадратов заключается в том, что оценка неизвестных параметров ищется из условия минимизации суммы квадратов ошибок измерения.
Рассмотрим линейный случай метода наименьших квадратов:
Пусть есть 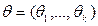 - вектор неизвестных параметров.
- вектор неизвестных параметров.
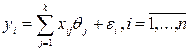 . (1)
. (1)
Ошибки 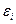 необязательно нормальные:
необязательно нормальные: 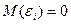 . Ошибки
. Ошибки 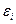 - некоррелированы
- некоррелированы 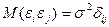 , где
, где 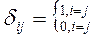 .
.
Перепишем зависимость (1) в матричной форме: 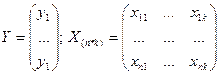 .
.
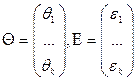 , тогда имеем
, тогда имеем 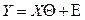 , в связи с этим:
, в связи с этим:
1. 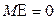 .
.
2. 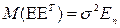 , где
, где 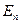 - единичная матрица n*n.
- единичная матрица n*n.
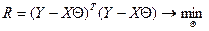 .
.
Наценку параметра 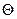 будем находить из условия:
будем находить из условия:
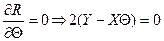 .
. 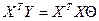 ,
, 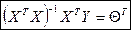 (*).
(*).
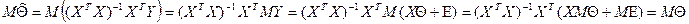
Следовательно, полученная оценка является не смещённой. Найдём вариацию оценки 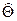 :
:
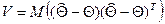 , т.к.
, т.к.
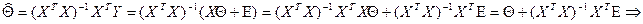
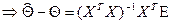 . Подставляя последнее выражение в соотношение для вариации,
. Подставляя последнее выражение в соотношение для вариации,
получим:
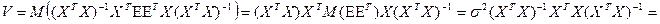
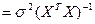 .
.
Сформулируем следующую теорему:
Теорема (Оптимальное свойство МНК-оценки): МНК оценка имеют наименьшую дисперсию в классе линейных несмещённых оценок.
МНК используется в задачах параметризации квадратов использованных в задачах оценки параметров между 2-я и более переменными.
Пример:
Пусть зависимость между 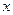 и
и 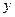 имеет вид:
имеет вид:
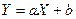 , где
, где 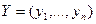 ,
, 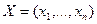 ,
, 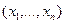 - значение
- значение
Требуется оценить МНК параметры 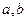 :
:
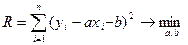 ,
, 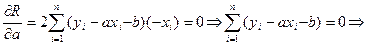
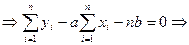
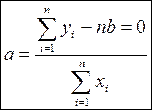 .
.
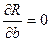 ,
, 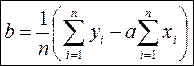 .
.
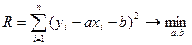 ;
; 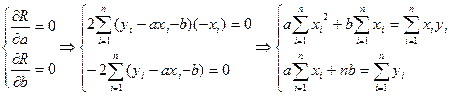 ,
,
Решая последнюю систему относительно 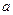 и
и 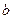 получим:
получим:
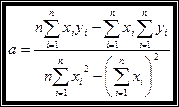
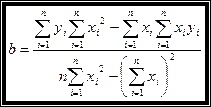 .
.
Обозначим: 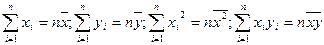 . Получим:
. Получим:
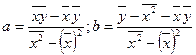 .
.
 2014-02-02
2014-02-02 913
913








