2014-02-02
332
Пусть дана выборка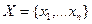 
. Проверяется следующая гипотеза: 
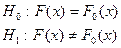, где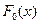 
- некоторая известная функция распределения. 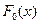может быть известна с точностью до неизвестного параметра. Гипотеза проверяется при заданном уровне значимости 
.
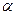Для построения критерия выше описанной гипотезы множество выборочных значений разбивается на k непересекающихся классов.
Определим число выборочных значений попавших в k-ый класс: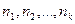 
.
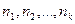сравнивается с теоретическими частотами 
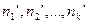. Теоретические частоты находятся по функции распределения 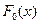следующим образом:
Пусть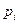 
- вероятность попадания значения в 
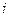-ый класс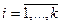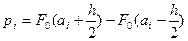, где 
: 
, где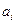 
- середина 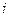-го класса, а 
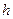- ширина класса, при 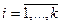. Теоретические частоты 
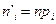, где .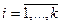
Если параметры теоретической функции распределения 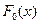известны, то величина
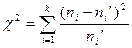, при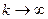 
стремится к 
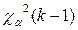. Получаем: 
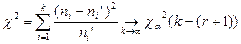, где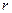 
- это число параметров.
Если выполняется неравенство вида: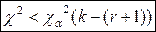 
, то принимаем гипотезу 
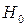, в противном случае гипотеза 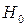отвергается.
