2014-02-02
957
Критерий согласия Колмогорова:
Пусть имеем: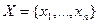 
, 
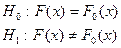, где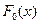 
- некоторая заданная функция распределения.
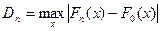, где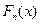 
- эмпирическая функция распределения по выборке 
.
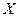Распределение величины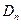 
определил Колмогоров: 
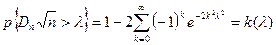, где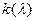 
- функция Колмогорова.
Задавая уровень значимости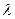 
из соотношения: 
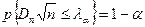можно найти критерий значения распределения Колмогорова (по таблице).
Т. о. применяя критерии Колмогорова:
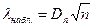и сравнивают его с табличным значением: 
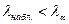, при заданном 
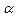, то говорят, что табличные значения распределены по закону 
.
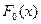Критерий согласия Колмогорова - Смирнова:
Со случайной величиной 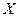проводят 2-е серии опытов. В результате получим 2 выборк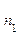и: 
и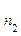 
(объём).
Пусть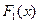 
и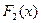 
функция распределения СВ 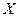в 1-ой и 2-ой серии соответственно.
Будем рассматривать следующие задачи:
Требуется проверить теорию: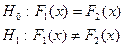 
.
Пусть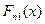 
и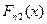 
- выборочные эмпирические функции распределения в 1-ом и 2-ом выборочном соответствии. Критерии Колмогорова – Смирнова заключается в следующем: 
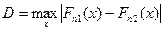. Если 
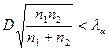, то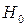 
принимается, в противном случаи принимается гипотеза 
.
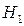Критическое значение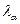 
при заданном значении 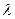определяется как и в случаи критерия Колмогорова.
