Задача регрессионного анализа.
Проверка гипотезы о распределении выборочных значений по закону Пуассона.
Пусть задана выборка 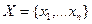 , причём:
, причём: 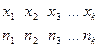 ,
, 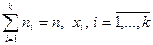 - равноотстоящие.
- равноотстоящие.
1. 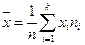
2. В качестве оценки параметра 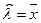 .
.
3. Найти предполагаемый закон Пуассона: 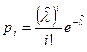 , где
, где 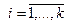 .
.
4. 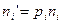 , где
, где 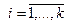 (теоретические частоты)
(теоретические частоты)
5. 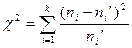 , но
, но 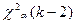 .
.
Если 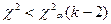 , то выборочное значение распределено по закону Пирсона.
, то выборочное значение распределено по закону Пирсона.
Рассмотрим следующую задачу:
Есть 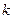 независимы переменных и зависящая от них переменная
независимы переменных и зависящая от них переменная 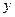 . Сами переменные могут быть случайными и при желании можем задать их значения. На величину
. Сами переменные могут быть случайными и при желании можем задать их значения. На величину 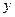 также влияют другие неподдающиеся точному фактору, а это значит, что величина
также влияют другие неподдающиеся точному фактору, а это значит, что величина 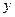 носит случайный характер.
носит случайный характер.
Нас будет интересовать методы экспериментального определения влияния переменных 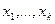 на
на 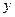 , а именно: определить по данным эксперимента вид зависимости:
, а именно: определить по данным эксперимента вид зависимости: 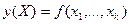 .
.
Задача регрессионного анализа состоит от экспериментально определённых коэффициентов регрессии вида: 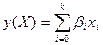 путём наблюдения за характером изменений входных переменных
путём наблюдения за характером изменений входных переменных 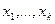 и выходного
и выходного 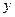 , служат методы активного и пассивного эксперимента.
, служат методы активного и пассивного эксперимента.
Пассивный эксперимент основан на регистрации контроля параметра в процессе нормальной работы объекта без внесений преднамеренных возмущений.
Активный эксперимент основан на использовании искомого возмущения вводимых в объект по заранее спланированной программе. При активном эксперименте ведение искомых возмущений позволяет быстро и целенаправленно вскрывать нужные зависимости между параметрами, но введение искомых возмущений может привести к нарушению нормального хода технологий.
При организованном числе экспериментов невозможно точно найти значение 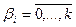 . Поэтому находят оценки этих коэффициентов
. Поэтому находят оценки этих коэффициентов 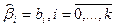 ,
, 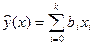 определяют оценку математического ожидания истинной функции
определяют оценку математического ожидания истинной функции 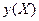 .
.
Для определения оценок коэффициентов 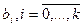 проводят серию экспериментов, в каждом из которых измеряют величины на входах и выходах исследованного объекта.
проводят серию экспериментов, в каждом из которых измеряют величины на входах и выходах исследованного объекта.
Рассмотрим 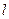 -ый эксперимент,
-ый эксперимент, 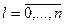 . Пусть
. Пусть 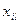 и
и 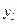 , где
, где 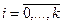 ,
, 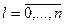 - значения величин
- значения величин 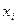 и
и 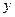 в этом эксперименте. Оценка
в этом эксперименте. Оценка 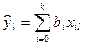 будет отличаться от измеренного значения
будет отличаться от измеренного значения 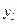 . Величины
. Величины 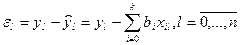 . Для определения коэффициентов
. Для определения коэффициентов 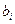 будет использован метод наименьших квадратов. В этом случаи оценки
будет использован метод наименьших квадратов. В этом случаи оценки 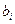 будут находится из условия:
будут находится из условия: 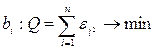 . Перейдём к матричной форме:
. Перейдём к матричной форме: 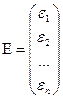 ,
, 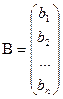 ,
, 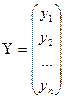 ,
, 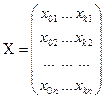 . Тогда наша зависимость запишется в виде:
. Тогда наша зависимость запишется в виде: 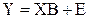 . Для использования метода наименьшего квадрата будем рассматривать следующую величину:
. Для использования метода наименьшего квадрата будем рассматривать следующую величину: 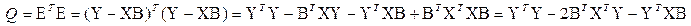 .
.
Минимум находим из условия: 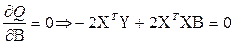 ,
, 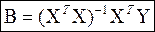 . Т.к. определение оценок коэффициентов
. Т.к. определение оценок коэффициентов 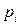 проводится по искажённым помехам экспериментальных данных, то для получения точных оценок нужно, что бы число экспериментов было
проводится по искажённым помехам экспериментальных данных, то для получения точных оценок нужно, что бы число экспериментов было 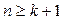 , где
, где 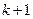 -число неизвестных параметров, т.к.
-число неизвестных параметров, т.к. 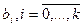 .
.
Определение: Разность между числом наблюдений 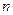 и числом неизвестных параметров
и числом неизвестных параметров 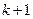 называется число степеней свободы эксперимента:
называется число степеней свободы эксперимента: 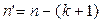 .
.
О правильности построений по экспериментальным данным регрессионной модели с уровнем надёжности 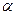 можно судить на основании
можно судить на основании 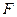 - критерия Фишера. Для этого определим отношение:
- критерия Фишера. Для этого определим отношение: 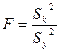 , где
, где 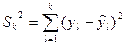 - дисперсия, характеризующая рассеяние эксперимента точек относительно уровня регрессии,
- дисперсия, характеризующая рассеяние эксперимента точек относительно уровня регрессии, 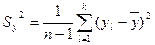 - дисперсия, характеризующая ошибку эксперимента,
- дисперсия, характеризующая ошибку эксперимента, 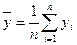 - выборочная средняя всех результатов эксперимента. Когда значение
- выборочная средняя всех результатов эксперимента. Когда значение 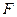 найдено, его сравнивают с табличными значениями
найдено, его сравнивают с табличными значениями 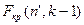 . Если
. Если 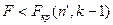 , то построенная модель считается адекватной.
, то построенная модель считается адекватной.
 2014-02-02
2014-02-02 566
566








