2014-02-02
1101
Определение: Ошибкой I-го рода называется ошибка, когда выносится решение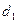 
(т.е в пользу гипотезы 
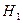), а на самом деле верна гипотеза 
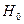. Ошибка обозначается: 
.
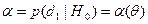Определение: Ошибкой II-го рода называется ошибка, когда выносится решение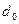 
(т.е в пользу гипотезы 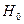), а на самом деле верна гипотеза 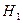. Ошибка обозначается: 
.
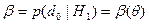Определение: Вероятность вынесения правильного решения 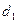в случаи, когда верна гипотеза 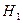, называется мощностью критерия: 
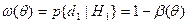. Желательно, что бы ошибка I-го и II-го рода были равны 0, но это невозможно. При уменьшении вероятности I-го рода мы увеличиваем вероятность ошибки II-го рода и наоборот.
Подход Неймона - Пирса к выбору решения функции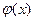 
заключается в следующем:
Функция 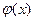выбирается следующим образом:
Вероятность ошибки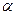 
, нужно делать такой, что бы она не превышала некоторого заданного значения, т.е. 
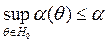, а мощность критерия: 
.
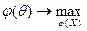Определение: Величина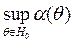 
называется размерностью критерия, 
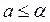- уровнем значимости.
В случаи 2-альтернативных простых гипотез рассмотрим следующую задачу: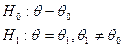 
;
.
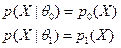Если функция 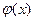- решающая функция, т.е. это вероятность вынесения решения в пользу решения 
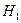, то по формуле полной вероятности можно записать: 
.
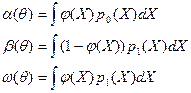Задавая уровень значимости 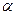решающую функцию 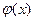мы ищем решая задачу: 
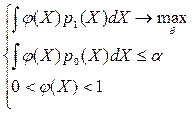. Данную задачу решает Лемма Неймана – Пирсона.
