Любое подмножество 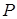 декартова произведения
декартова произведения 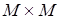 называется (бинарным) отношением на множестве M.
называется (бинарным) отношением на множестве M.
Пусть 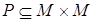 и
и 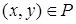 . Тогда пишут
. Тогда пишут 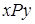 .
.
Приведем основные свойства отношения P, заданного на множестве M:
рефлексивность: для всех x Î M выполняется xPx;
антирефлексивность: для всех x Î M неверно, что xPx;
симметричность: для всех x, y Î M из xPy следует, что yPx;
асимметричность: для всех x, y Î M из xPy следует неверно, что yPx;
антисимметричность: для всех x, y Î M из xPy и yPx следует, что x = y;
транзитивность: для всех x, y, z Î M из xPy и yPz следует, что xPz;
связность: для всех x, y Î M верно, что xPy, или yPz или x = y.
3. Обратное отношение. Композиция отношений. Над отношениями, заданными на множестве M, можно производить те же операции, что над множествами: объединение 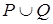 , пересечение
, пересечение 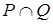 , дополнение
, дополнение 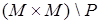 .
.
Отношение 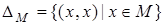 называется диагональю множества M.
называется диагональю множества M.
Отношение 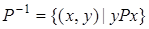 называется обратным к отношению
называется обратным к отношению 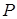 .
.
Отношение 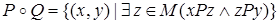 называется композицией отношений
называется композицией отношений 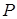 и
и 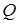 .
.
С помощью операций над отношениями можно охарактеризовать свойства отношений: отношение P на множестве M
рефлексивно тогда и только тогда, когда 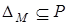 ;
;
антирефлексивно тогда и только тогда, когда 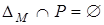 ;
;
симметрично тогда и только тогда, когда 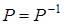 ;
;
асимметрично тогда и только тогда, когда 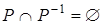 ;
;
антисимметрично тогда и только тогда, когда 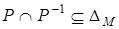 ;
;
транзитивно тогда и только тогда, когда 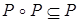 ;
;
связно тогда и только тогда, когда 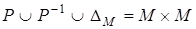 .
.
 2014-02-02
2014-02-02 1962
1962








