Отношения эквивалентности, фактор - множества

Рефлексивное, симметричное и транзитивное отношение называется эквивалентностью.

Пусть ~ есть эквивалентность на множестве M, а x Î M. Тогда множество [ x ]={ y | y ~ x } называется классом эквивалентности, порожденным элементом x.

Фактор-множество множества 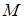относительно эквивалентности ~ – это семейство всех классов эквивалентности: M /~={[ x ]| x Î M }.

Теорема. Пусть на множестве M задана эквивалентность ~. Тогда семейство всех классов эквивалентности [ x ], x Î M, есть разбиение M на классы.

Доказательство. Проверим выполнение всех трех условий определения разбиения множества на попарно непересекающиеся классы:

1) для всех x Î M класс [ x ]¹Æ, [ x ]Í M;

2) для всех x, y Î M классы [ x ] и [ y ] не пересекаются: [ x ]Ç[ y ]=Æ, где x ¹ y;

3) объединение всех классов [ x ], x Î M совпадает с множеством M.

Условие 1) следует из рефлексивности отношения ~.

Условие 2) из транзитивности и симметричности отношения ~. Действительно, если z Î[ x ], z Î[ y ], x, y, z Î M, то z ~ x, z ~ y, x ~ z, x ~ y, [ x ]=[ y ].