Представим аналитический спектральный сигнал в экспоненциальной форме:
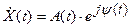 |
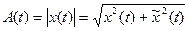 - действительный случайный процесс, называемый огибающей сигнала X(t).
- действительный случайный процесс, называемый огибающей сигнала X(t). 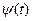 - действительный случайный процесс, называемый полной фазой или фазой сигнала. Для ψ(t) справедливо следующее равенство:
- действительный случайный процесс, называемый полной фазой или фазой сигнала. Для ψ(t) справедливо следующее равенство:
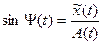 ,
, 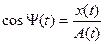
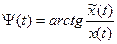
Огибающая и фаза полностью определяется (для случайного процесса в вероятностном смысле) действительным сигналом X(t). Из определения огибающей видно, что A(t)>>|X(t)|. А в тех точках, где имеет место равенство A(t)=X(t) сигнал и его огибающая имеют одинаковые производные 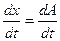 . Понятие огибающей и полной фазы процесса можно проиллюстрировать, изобразив сигнал в виде случайного векторного процесса на комплексной плоскости. На рисунке показано одна из реализаций вектора x(t) в момент t=0.
. Понятие огибающей и полной фазы процесса можно проиллюстрировать, изобразив сигнал в виде случайного векторного процесса на комплексной плоскости. На рисунке показано одна из реализаций вектора x(t) в момент t=0.
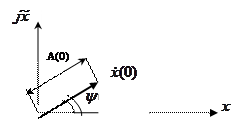 |
Длина этого вектора =А(0), а угол между ним и действительной осью составляет 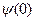 .С течением времени конец вектора перемещается по некоторой траектории так, что в любой момент его длина равна A(t) и он образует
.С течением времени конец вектора перемещается по некоторой траектории так, что в любой момент его длина равна A(t) и он образует 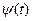 с действительной осью.
с действительной осью.
Угловая скорость вектора 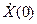 -
- 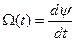 называется мгновенной частотой сигнала. Ее можно выразить через действительный сигнал X(t) и сопряженный с ним сигнал
называется мгновенной частотой сигнала. Ее можно выразить через действительный сигнал X(t) и сопряженный с ним сигнал 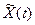 , дифференцируя по t выражение для
, дифференцируя по t выражение для 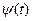 :
:
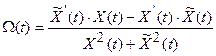 ,
,
где “ ’ ” означает производную по времени.
Выберем произвольную частоту ω0. 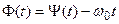 . Тогда:
. Тогда:
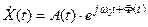 | (*) |
Случайная функция 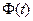 называется мгновенной начальной фазой сигнала относительно частоты ω0., она зависит от выбора ω0.
называется мгновенной начальной фазой сигнала относительно частоты ω0., она зависит от выбора ω0.
Действительный сигнал X(t) и сопряженный с ним 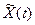 можно представить в квазигармонической форме непосредственно вытекающей из экспоненциального представления аналитического сигнала:
можно представить в квазигармонической форме непосредственно вытекающей из экспоненциального представления аналитического сигнала:
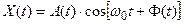
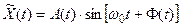
Еще одно свойство аналитического сигнала: если все гармонические составляющие всех реализаций случайного процесса X(t) сдвинуть по фазе на одинаковый угол 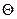 , то полученный при этом процесс:
, то полученный при этом процесс:
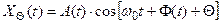
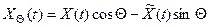
Аналогично, при повороте на угол (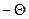 ):
):
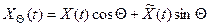
 2014-02-02
2014-02-02 1179
1179








