Зная функцию распределения исходного случайного процесса X(t), можно обычными методами теории вероятности найти функцию распределения для всех вновь введенных процессов: 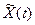 ,
, 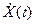 , A(t),
, A(t), 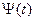 ,
, 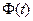 ,
, 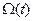 , Aс(t), Aк(t).
, Aс(t), Aк(t).
В общем случаи эта не простая задача, поэтому рассмотрим частный случай, когда X(t)-центрированный стационарный Гауссовский процесс.
Известно, что процесс, полученный в результате линейного преобразования Гауссовского процесса, также является Гауссовским, т.к. преобразования Гильберта линейно, можно утверждать, что 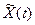 также Гауссовский процесс.
также Гауссовский процесс.
Процессы Aс(t) и Aк(t) представляют собой линейные комбинации процессов X(t) и 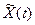 , поэтому их распределение будет Гауссовским. Поскольку
, поэтому их распределение будет Гауссовским. Поскольку 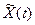 отличается от X(t) только фиксированным сдвигом фаз всех гармонических составляющих, то
отличается от X(t) только фиксированным сдвигом фаз всех гармонических составляющих, то
1. 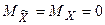 , т.к. математическое ожидание имеет смысл среднего значения процесса, который при таком преобразовании не меняется.
, т.к. математическое ожидание имеет смысл среднего значения процесса, который при таком преобразовании не меняется.
2. 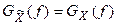 , т.к. энергетический спектр не зависит от фазовых соотношений.
, т.к. энергетический спектр не зависит от фазовых соотношений.
3. 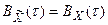 , вытекает из второго пункта теоремы Винера – Хинчина.
, вытекает из второго пункта теоремы Винера – Хинчина.
|
|
|
4. 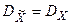 , т.к. D=B(0).
, т.к. D=B(0).
Процессы X(t) и 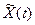 являются Гауссовскими и в совпадающие моменты времени между собой не коррелированны, следовательно, они не зависимые. Поэтому, совместную плотность вероятностей X(t) и
являются Гауссовскими и в совпадающие моменты времени между собой не коррелированны, следовательно, они не зависимые. Поэтому, совместную плотность вероятностей X(t) и 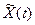 характеризующую аналитический сигнал
характеризующую аналитический сигнал 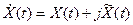 в одном сечении t можно записать так:
в одном сечении t можно записать так:
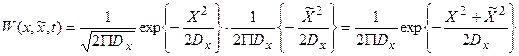
Дисперсия аналитического сигнала:
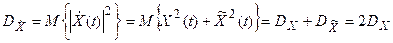
Процессы 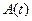 и
и 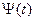 также стационарны, но поскольку они получены из X(t) и
также стационарны, но поскольку они получены из X(t) и 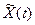 с помощью нелинейных операций, они не являются Гауссовскими. Найдем совместную интегральную функцию распределения А и
с помощью нелинейных операций, они не являются Гауссовскими. Найдем совместную интегральную функцию распределения А и 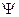 в некотором сечении t, т.е. функцию
в некотором сечении t, т.е. функцию 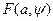 .
.
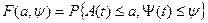
Геометрическая интерпретация этой задачи представлена на рисунке:
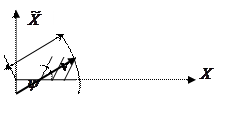 |
По оси ординат отложены значения 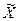 , а по оси абсцисс X. искомая функция распределения является вероятностью того, что коней вектора представляющего аналитический сигнал
, а по оси абсцисс X. искомая функция распределения является вероятностью того, что коней вектора представляющего аналитический сигнал 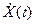 находится внутри заштрихованной зоны. Для нахождения функции распределения
находится внутри заштрихованной зоны. Для нахождения функции распределения 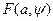 , можно проинтегрировать
, можно проинтегрировать 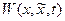 по области V. Перейдем к полярной системе координат
по области V. Перейдем к полярной системе координат 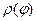 используя известные формулы:
используя известные формулы:
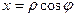
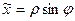
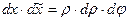
При этом имеем:
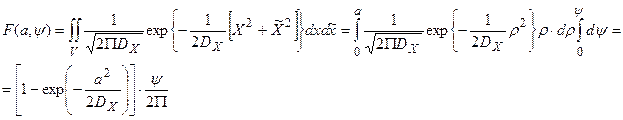
Двумерная интегральная функция распределения представляет собой произведение двух одномерных функций:
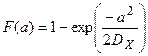
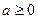
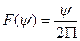
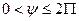
Это означает, что огибающая 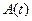 и
и 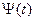 в одном сечении независимы. Плотность распределения огибающей найдем как производную интегральной функции распределения:
в одном сечении независимы. Плотность распределения огибающей найдем как производную интегральной функции распределения:
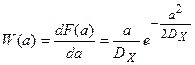

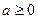
Это известное распределение Релея, график которого показан на рисунке совместно с графиком Гауссовского распределения 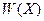 :
:
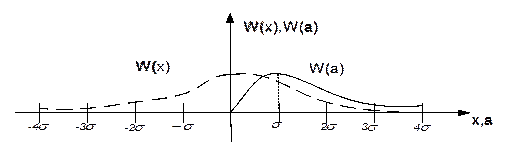
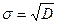
Наиболее вероятностные значения 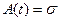 . Математическое ожидание -
. Математическое ожидание - 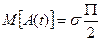 . Дисперсия -
. Дисперсия - 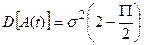 . Для плотности распределения фазы имеем:
. Для плотности распределения фазы имеем:
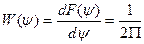
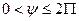
Следовательно, фаза стационарного централизованного Гауссовского процесса распределена равномерно на интервале (0,2π).
|
|
|

Мгновенная начальная фаза 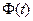 рассмотревшего процесса также равномерно распределена на интервале протяженностью 2π. Действительно, можно отыскать совместную интегральную функцию распределения
рассмотревшего процесса также равномерно распределена на интервале протяженностью 2π. Действительно, можно отыскать совместную интегральную функцию распределения 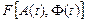 исходя из совместной плотности распределения процесса
исходя из совместной плотности распределения процесса 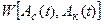 . Процессы Aс(t) и Aк(t) являются центрированными Гауссовскими процессами не зависимыми в совпадающие моменты времени, причем
. Процессы Aс(t) и Aк(t) являются центрированными Гауссовскими процессами не зависимыми в совпадающие моменты времени, причем 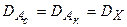 , поэтому совместная плотность вероятности
, поэтому совместная плотность вероятности 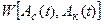 определяется выражением аналогичным
определяется выражением аналогичным 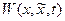 в котором символы X и
в котором символы X и 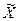 заменены на Aс и Aк. Повторяя только что проведенные рассуждения и выкладки заменой X,
заменены на Aс и Aк. Повторяя только что проведенные рассуждения и выкладки заменой X, 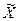 ,
,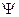 на Aс, Aк,
на Aс, Aк,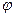 найдем плотность распределения для A(t) и равномерную плотность распределения
найдем плотность распределения для A(t) и равномерную плотность распределения 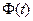 .
.
 2014-02-02
2014-02-02 1110
1110
