2014-02-02
1559
Введенные понятия можно распространить и на случайные процессы. Ансамбль комплексных функций действительной переменной t -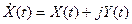 
с заданными n-мерными распределениями вероятностей представляет собой комплексный случайный процесс, который можно рассматривать как совокупность двух действительных процессов X(t) и Y(t). Распределение n-го порядка процесса 
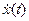задается 2n-мерным совместным распределением процессов X(t) и Y(t).
Математическое ожидание комплексного случайного процесса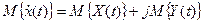 
и представляет собой в общем случае комплексную функцию времени. Его дисперсия 
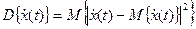также в общем случае является функцией времени, но не комплексной, а действительной и к тому же неотрицательной.
Функция корреляции комплексного случайного процесса определяется как:
,
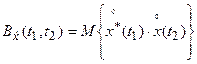
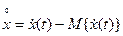где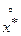
– центрированный процесс (знак “*” означает комплексное сопряжение).
В общем случае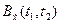
является комплексной функцией двух действительных аргументов, при этом:
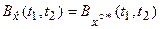
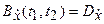
Комплексный случайный процесс стационарен в широком смысле, если его математическое ожидание не зависит от времени, а функция корреляции зависит только от разности τ=t2–t1. Из этого следует, что и дисперсия стационарного комплексного процесса не зависит от времени.
Комплексный случайный процесс 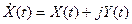называют аналитическим, если
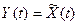, где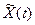 
- есть преобразование Гильберта от X(t). Аналитические случайные процессы обладают свойствами аналогичными детерминированным аналитическим сигналам. В частности, если действительный случайный сигнал Х(t) имеет энергетический спектр Gx(f), то у аналитического сигнала, соответствующего X(t) энергетический спектр равен:
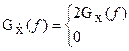
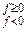
Таким образом, спектральная плотность мощности аналитического сигнала совпадает с односторонним энергетическим спектром его действительной части.
Важным параметром аналитического сигнала является функция взаимной корреляции между процессами X(t) и: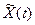
  |
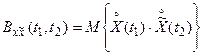Для стационарного аналитического сигнала она зависит только от разности фаз τ = τ2– τ1, причем можно показать, что при τ=0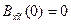 
. Таким образом, функции X(t) и 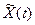не коррелированны в совпадающие моменты времени.
