Параграф 1.10: Комплексное и квазигармоническое представление сигналов.
В электротехнике широко используется символический метод, в соответствие с которым принято представлять гармонические колебания (ток, напряжение) в форме:
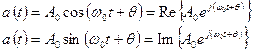
Такой прием позволяет заменить выполнение трудоемких алгебраических операций с тригонометрическими функциями более простыми действиями над комплексными величинами, облегчает решение многих задач и приводит к правильным результатам, если полученное комплексное решение заменить его действительной или мнимой частью.
В современной технике связи представление колебаний в комплексной форме получило дальнейшее развитие и распространено на негармонические сигналы. Обобщением символического метода является представление любого сложного сигнала комплексной функции:
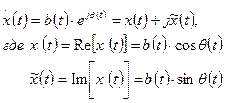
В частном случае гармонического сигнала 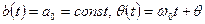 .
.
При этом сопряженный сигнал 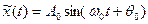 ,отличается от действительного сигнала
,отличается от действительного сигнала 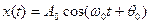 только сдвигом фазы на (
только сдвигом фазы на (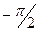 ).
).
В общем случае негармонического сигнала x(t) также определим сопряженный сигнал 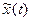 как результат поворота фаз всех гармонических составляющих спектральной характеристики на (
как результат поворота фаз всех гармонических составляющих спектральной характеристики на (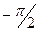 ). Иначе говоря, если x(t) можно представить интегралом Фурье в тригонометрической форме:
). Иначе говоря, если x(t) можно представить интегралом Фурье в тригонометрической форме:
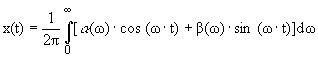
то 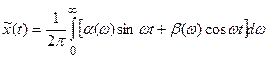 ,
,
где 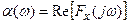 ,
, 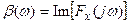
Можно показать, что два сигнала x(t) и, 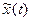 удовлетворяющие этим условиям, связанны между собой во временной области интегральными преобразованиями, называемыми преобразованиями Гильберта:
удовлетворяющие этим условиям, связанны между собой во временной области интегральными преобразованиями, называемыми преобразованиями Гильберта:
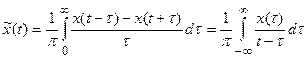
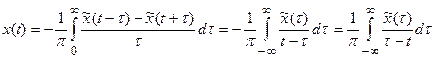
Первая из этих формул выражает прямое преобразование Гильберта, а вторая - обратное преобразование Гильберта.
Комплексный сигнал 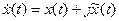 называют аналитическим сигналом, если
называют аналитическим сигналом, если 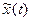 есть преобразование Гильберта от
есть преобразование Гильберта от 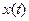 .
.
Определим, как связан спектр аналитического сигнала 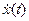 и спектр исходного сигнала x(t). Так как фазы всех составляющих спектральной плотности
и спектр исходного сигнала x(t). Так как фазы всех составляющих спектральной плотности 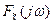 сопряженного сигнала
сопряженного сигнала 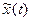 в области положительных частот сдвинуты на (
в области положительных частот сдвинуты на (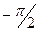 ) относительно,
) относительно, 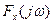 , а умножение на j означает сдвиг фазы на (
, а умножение на j означает сдвиг фазы на (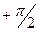 ), то
), то 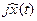 имеет в области положительных частот такой же спектр, как и x(t). В области же отрицательных частот преобразование Гильберта соответствует повороту фаз на (
имеет в области положительных частот такой же спектр, как и x(t). В области же отрицательных частот преобразование Гильберта соответствует повороту фаз на (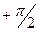 ), и поэтому спектре
), и поэтому спектре 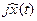 фазы с отрицательными частотами сдвинуты на
фазы с отрицательными частотами сдвинуты на 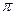 относительно спектра x(t).
относительно спектра x(t).
В результате спектр аналитического сигнала в области отрицательных частот равен нулю, а в области положительных частот спектры x(t) и 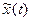 складываются в одной фазе.
складываются в одной фазе.
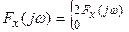
 2014-02-02
2014-02-02 2134
2134
