Электродвижущая сила гальванического элемента (ЭДС)

Электрическая работа, получаемая с помощью гальванического элемента, будет максимальной, когда элемент работает в условиях, наиболее близких к обратимым. Максимальная разность потенциалов электродов данного гальванического элемента, которая определяется в условиях равновесия, называется его электродвижущей силой (ЭДС). Она равна разности равновесных потенциалов катода и анода элемента.

При стандартных условиях:

ЭДС⁰ = Dj⁰ = j⁰_катода -j⁰_анода. (7.3)

Пример 10. Вычислить ЭДС гальванического элемента, составленного из магниевого и свинцового электродов, в котором [Mg²⁺] = 0,1 M; [Pb²⁺] = 0,001 M.

Решение. j⁰ Mg²⁺/Mg = -2,37 В; j⁰ Pb²⁺/Pb = -0,13 B (табл. 7.1); j ⁰ магниевого электрода меньше, т.е. Mg является более активным металлом, поэтому в гальваническом элементе магний будет анодом, а свинец - катодом.

На электродах будут протекать следующие процессы:

А: Mg - 2e = Mg²⁺,

К: Pb²⁺ + 2e = Pb⁰.

Схема гальванического элемента записывается так: Mg½Mg²⁺?Pb²⁺½Pb.

Для расчета ЭДС необходимо найти электродные потенциалы.

Согласно уравнению (7.2):

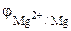= j⁰ + 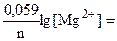-2,37 + 0,0295^.lg 0,1 = -2,4 B;

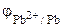= -0,13 + 0,0295^.lg 0,001 = -0,13 + 0,0295·(-3) = -0,22 В.

ЭДС = j _кат - j _ан = -0,25 - (-2,4) = 2,15 В.

Пример 11. Определить ЭДС гальванического элемента, составленного из серебряных электродов, опущенных в 0,0001 М и 0,1 М растворы AgNO₃.

Решение. Гальванический элемент может быть составлен не только из различных, но и одинаковых электродов, погруженных в растворы одного и того же электролита различной концентрации (концентрационные элементы). Найдем электродные потенциалы по формуле Нернста (7.2):

j ¹_{Ag+ / Ag} = j⁰ + 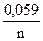×lg[Ag⁺] = 0,8 + 0,059 × lg0,001 = 0,8 + 0,059×(-3) = 0,62 В,

j ² _{Ag+ / Ag} = 0,8 + 0,059×lg0,1 = 0,8 - 0,059 = 0,74 В.

Поскольку j¹ < j², электрод, опущенный в 0,001 М раствор, будет являться анодом:

ЭДС = j _кат - j _ан = 0,74 - 0,62 = 0,12 В.

Схема такого гальванического элемента записывается так:

(-) Ag½ AgNO₃(0,001М)? AgNO₃(0,1М) ½ Ag(+).

Как уже было показано на примере водородного электрода, электроды, а следовательно, и гальванические элементы могут быть созданы не только для реакции окисления-восстановления металлов, но и для любых веществ и окислительно-восстановительных реакций, происходящих в растворах или расплавах.

Например, для реакции в растворе:

2KMnO₄ + 5Na₂SO₃ + 3H₂SO₄ = 2MnSO₄ + 5Na₂SO₄ + K₂SO₄ + 3H₂O

процессы окисления и восстановления можно разделить в виде полуреакций:

на аноде: 5 ½ SO₃^2- + H₂0 = SO₄^2- + 2H⁺ + 2?; (0,17 В),

на катоде: 2 ½ MnO₄^- + 8H⁺ + 5e = Mn²⁺ + 4H₂O (1,51 В).

Суммируем:

2MnO₄^- + 5SO₃^2- + 6H⁺ + 10? = 2Mn²⁺ + 5SO₄^2- + 3H₂O + 10?.

Т окообразующая реакция:

2MnO₄^- + 5SO₃^2- + 6H⁺ = 2Mn²⁺ + 5SO₄^2- + 3H₂O.

Для осуществления таких реакций обычно используют катализатор, который одновременно является проводником электронов, например платину (рис. 7.3).

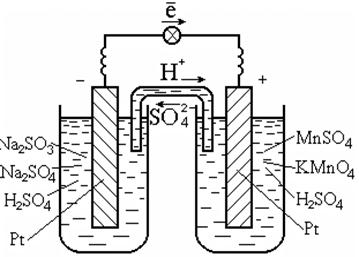
Рис. 7.3. Гальванический элемент на окислительно-восстановительной реакции в растворе

Схема гальванического элемента:

Pt | SO₃^2-, SO₄^2-, H⁺|| MnO₄^-, Mn²⁺, H⁺| Pt.

Значения стандартных электродных потенциалов полуреакций приводятся в справочниках.

ЭДС такого элемента при стандартных условиях можно определить как разность потенциалов для полуреакций восстановления (окислителя) и окисления (восстановителя).

ЭДС = Dj⁰ = j⁰ (MnО₄^-/ Mn²⁺) - j⁰ (SO₄^2- / SO₃^2-) = 1,51 - 0,17 = 1,34 B.

Если при этом ЭДС положительна, то реакция возможна при стандартных условиях, так как DG реакции и электрическая работа (ЭДС) связаны между собой соотношением:

DG = -n×F×Dj,

где F - постоянная Фарадея (заряд, переносимый одним молем элементарных зарядов (F = 96485, или»96500Кул/моль экв);

n - заряд, переносимый одной частицей (для Zn²⁺ и Cu²⁺ n = 2);

Dj = j_катода - j_анода = j_ок-ля - j_{восст-ля.}

Таким образом, разность потенциалов на электродах можно не только непосредственно измерить, но и вычислить из чисто химических экспериментальных данных. В случае нестандартных условий потенциал электрода и ЭДС элемента рассчитывается по формуле Нернста (7.1).

Например, для рассматриваемой реакции:

,

(n = 10). Так как концентрации реагентов находятся под знаком логарифма, то зависимость Dj от них слабая.