Принятие решений в условиях риска. Предположим, что Х, Y – случайные величины, которые «связаны» какой-то зависимостью

Задача о линейной регрессии

Предположим, что Х, Y – случайные величины, которые «связаны» какой-то зависимостью. Наша цель – построить такую функцию, которая бы позволяла для любого значения аргумента х «угадывать» значение случайной величины Y, соответствующее ситуации «{ X = x }»:

y = а + kx (1),

где а, k – функции от выборки, т.е. а = a (X ₁ ,Y ₁,..., X_n,Y_n),

k = k (X ₁ ,Y ₁,..., X_n,Y_n) и X ₁,..., X_n; Y ₁,..., ,Y_n - выборочные значения величин Х и Y, соответственно.

Предположим, что у второго игрока имеется стратегия:

θ = (X ₁ ,Y ₁,..., X_n,Y_n),

а первый игрок в качестве стратегии δ = (a, k) может использовать любую линейную функцию

δ = a + kх

При рассмотрении этой задачи как задачи о наименьшихквадратах, функция платежей задается так:

Тогда решением задачи о наименьших квадратах будет стратегия δ * = (a*,k*), для которой потери будут наименьшими:

.

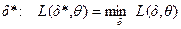Для нахождения экстремума составляется система:

.

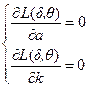Решая эту систему, находим

где 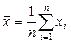– выборочное среднее Х;

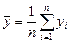– выборочное среднее Y;

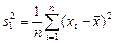– выборочная дисперсия Х;

– выборочный центрированный смешанный момент.

Таким образом, искомая линейная функция имеет вид:

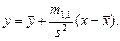
Рассмотрим другую постановку этой задачи – как задачу о линейной регрессии. Пусть Х – неслучайная величина, а Y нормально распределенная случайная величина с параметрами

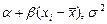
Линейную функцию (1) будем искать в виде

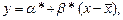
где α*, β* – какие-то оценки для параметров α, β. Поскольку оценки максимального правдоподобия обладают многими хорошими свойствами, остановимся на них.

Для построения оценок максимального правдоподобия рассмотрим функцию правдоподобия:

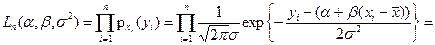
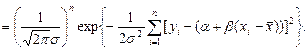
Логарифмическая функция правдоподобия:

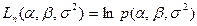Составляется система:

.

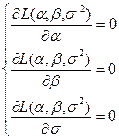Решения этой системы и будут искомыми оценками:

Таким образом, искомая линейная функция найдена:

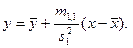
В данном подходе прогнозируется среднее значение случайной величины Y.

Задачи к § 12

12.1. Для исследования зависимости объемов производства (Y) от основных фондов (Х) получены данные по 8 предприятиям (в млн. руб.) за год:

(12, 210), (17, 220), (22, 230), (27,240),

(32, 250), (37, 260), (42, 270), (47, 280).

Найти уравнение линейной регрессии Y по X, отражающее зависимость объема производства от основных фондов.

12.2. Рассмотрим данные по совокупному денежному доходу населения (X) и по величине прожиточного минимума (Y) с 1992 по 1998 гг:

(7,1; 1,9), (79,9; 20,6), (360,9; 86,6), (942,3; 264,1),

(1374,5; 369,4), (1643,3; 411,2), (1700,4; 493,3).

Найти уравнение линейной регрессии Y по X, построить линию регрессии.

Как и в случае принятия решения в условиях неопределенности здесь решение принимается в условиях ограниченности или неточности информации. Степень неполноты данных выражается через функцию распределения. С точки зрения наличия исходных данных определенность и неопределенность представляет два крайних случая, а риск определяет промежуточную ситуацию.

Мы будем рассматривать следующие критерии принятия решения в условиях риска:

1) критерий ожидаемого значения (прибыль или расход);

2) комбинация ожидаемого значения и дисперсии;

3) критерий известного предельного уровня;

4) критерий наиболее вероятного события в будущем.

1. Критерий ожидаемого значения

Количественно этот критерий можно выразить в денежных единицах или в единицах полезности денег. Продемонстрируем это на примере. Предположим, что инвестиции $20 тыс. дают с равными вероятностями либо нулевой доход, либо $100 тыс. В денежных единицах ожидаемый доход составляет:

0,5·0 + 0,5·100 – 20 = $30 тыс.

Можно принять решение о вложении денег, однако это решение не в равной степени приемлемо для всех вкладчиков. Допустим имеются два вкладчика А и В. У А средства ограничены и потеря $20 тыс. приведет его к банкротству. В имеет средства, значительно превышающие $20 тыс., это бездействующий капитал и он может рисковать.

Предположим, что Z – случайная величина с математическим ожиданием E Z и дисперсией D Z. Пусть имеется выборка z ₁, z ₂,…, z_n объема n. Тогда выборочное среднее равно .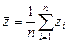

Выборочное среднее имеет дисперсию

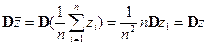
При n → ∞ .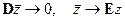

Отсюда, можно сделать следующий вывод: использование критерия ожидаемого значения допустимо лишь в том случае, когда одно и то же решение приходится принимать достаточно большое число раз.

Пример 1. Предположим, что есть необходимость профилактического ремонта оборудования. Требуется принять решение о том, когда следует проводить ремонт какого-либо станка чтобы минимизировать потери. Если весь временной отрезок разбит на равные периоды, то решение заключается в определении оптимального числа периодов между двумя ремонтами.

Предположим, что имеется n станков, через Т интервал времени выполняется профилактический ремонт всех n станков.

Определить оптимальное значение Т, при котором минимизируются затраты на ремонт вышедших из строя станков и проведение профилактического ремонта в расчете на один интервал времени.

Пусть p_t – вероятность выхода из строя одного станка в момент времени Т; n_t – случайная величина, число вышедших из строя станков (имеет биномиальное распределение с параметрами n, p_t, таким образом математическое ожидание E n_t = np_t); c ₁ – затраты на ремонт вышедшего из строя станка; c ₂ – затраты на профилактический ремонт; E C(T) – ожидаемые затраты за один интервал времени. Из условий получим

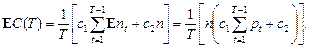
Требуется найти значение Т, удовлетворяющее условиям

.

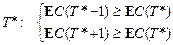Покажем это на нашем примере.

Пусть c₁ = 100, c₂ = 10, n = 50. Составим следующую таблицу:

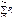T	Pt		EC(T)
	0,05
	0,07	0,05
	0,10	0,12	366,7
	0,13	0,22
	0,18	0,35

Из таблицы видно, что Т* = minT = 366,7. Т.е. ремонт следует производить через 3 периода.

2. Критерий ожидаемое значение – дисперсия

Предположим, что z – случайная величина с дисперсией D z. Выборочное среднее 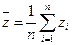имеет дисперсию .

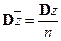Если дисперсия D z уменьшается, то дисперсия 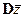также уменьшается, и это означает, что вероятность того, что 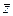будет приближаться к E z, увеличивается.

В условиях этого критерия выбирается:

max{ E z – k D z} или min{ E z + k D z},

где k – уровень не склонности к риску (постоянная величина).

Пример 2. В условиях предыдущего примера посчитаем дисперсию затрат за один период времени.

,

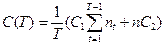где n_t – случайная величина, которая имеет биномиальное распределение (n_t ~ D n_t = np_t(1-p_t)).

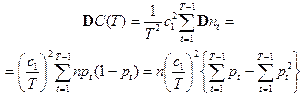
Выбираем то значение Т, которое удовлетворяет:

min{ E C(T) + k D C(T)}.

Пусть k = 1, c₁ = 100, c₂ = 10, n = 50.

T	pt	pt2		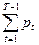	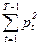EC(T)+DC(T)
	0,05	0,0025
	0,07	0,0049	0,05	0,025	6312,5
	0,10	0,01	0,12	0,074	6622,22
	0,13	0,0169	0,22	0,0174	6731,25
	0,18	0,0324	0,35	0,0343

Из таблицы находим Т* = minT = 500.