Определение 1. Двумерная случайная величина (x 1, x 2) называется дискретной, если x 1 и x 2 являются дискретными случайными величинами.
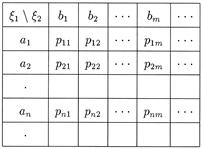 |
Такая случайная величина имеет следующую таблицу распределения:
где a 1, a 2, …, an … — значения случайной величины x 1; b 1, b 2, …, bn, … — значения случайной величины x 2; a pij = P (x 1 = ai, x 2 = bj) — совместные вероятности значений (x 1, x 2).
По этой таблице легко определить распределение вероятностей каждой из случайных величин x 1 и x 2 (эти распределения называются частными или маргинальными):
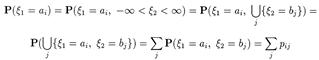 |
для любого i = 1, 2,..., п,...; аналогичными рассуждениями получим
Нетрудно определить функцию распределения Fx (x 1, x 2), где x =(x 1, x 2).
Ясно, что
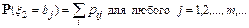 |
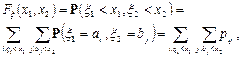
т.е. необходимо просуммировать рij по тем значениям i и j, для которых ai < x 1, bj < x 2.
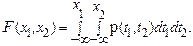 |
Определение 2. Двумерная случайная величина (x 1, x 2) называется непрерывной, если существует такая неотрицательная, интегрируемая на плоскости функция p(t 1, t 2), называемая двумерной плотностью (или совместной плотностью распределения случайных величин x 1 и x 2), что имеет место
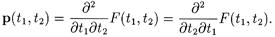 |
Если здесь предположить, что p(t 1, t 2), непрерывная функция по обоим аргументам, тогда
Приведем некоторые свойства совместной плотности распределения случайных величин x 1 и x 2.
1) p(t 1, t 2) ³ 0.
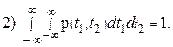 |
3) P ((x 1, x 2) Î D) = òò D p(t 1; t 2) dt 1 dt 2 где D Î Â 2 — некоторая область.
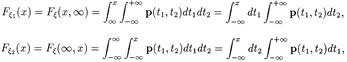 |
Далее, воспользовавшись свойством 3 двумерной функции распределения (см. 2.4.1), имеем
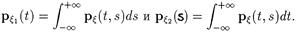 |
и дифференцируя, получаем выражения для одномерных плотностей:
Пример 1. Фирма выпускает мини-заводы по производству хлеба. На рекламу может быть израсходовано определённое количество средств. В таблице приведено возможное количество проданных в течение месяца заводов (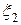 ) и объём средств, израсходованных на рекламу (
) и объём средств, израсходованных на рекламу (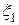 ). Каждой паре значений (ai,bj) случайных величин (
). Каждой паре значений (ai,bj) случайных величин (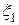 ,
,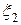 ) поставлена в соответствие вероятность
) поставлена в соответствие вероятность 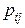 появления этой пары.
появления этой пары.
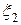 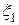 | |||
| 0,12 | 0,15 | 0,10 | |
| 0,08 | 0,10 | 0,12 | |
| 0,05 | 0,10 | 0,18 |
Требуется составить таблицы распределения вероятностей для каждой из величин 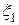 и
и 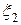 и выразить условный закон распределения вероятностей величины
и выразить условный закон распределения вероятностей величины 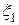 при
при 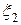 = 2.
= 2.
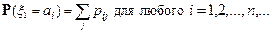 |
Воспользуемся формулами
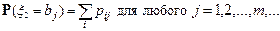 |
Таким образом, вероятность события
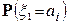 равна сумме вероятностей
равна сумме вероятностей 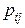 в i – м столбце, а вероятность
в i – м столбце, а вероятность 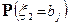 равна сумме вероятностей
равна сумме вероятностей 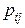 в j - й строке. В результате получаем таблицы распределения вероятностей:
в j - й строке. В результате получаем таблицы распределения вероятностей: 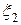 | |||
| P | 0,25 | 0,35 | 0,4 |
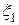 | |||
| P | 0,37 | 0,3 | 0,33 |
Находим условные вероятности величины 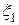 при
при 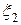 =2:
=2:
P(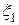 =1/
=1/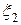 =2)=P (
=2)=P (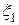 =1,
=1,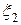 =2)/P (
=2)/P (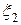 =2)=0,10/0,4=0,25;
=2)=0,10/0,4=0,25;
P(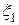 =2/
=2/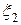 =2)=P (
=2)=P (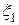 =2,
=2,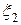 =2)/P (
=2)/P (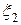 =2)=0,12/0,4=0,30;
=2)=0,12/0,4=0,30;
P(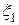 =3/
=3/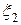 =2)=P (
=2)=P (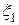 =3,
=3,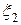 =2)/P (
=2)/P ( =2)=0,18/0,4=0,45.
=2)=0,18/0,4=0,45.
Пример 2. Пусть плотность распределения случайного вектора x = (x 1, x 2) постоянна в области D ={ a 1£ t 1£ b 1, a 2£ t 2£ b 2}, т.е.
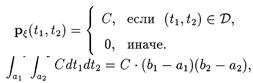 |
Найдем С, пользуясь свойством 2 совместной плотности:
Отсюда находим С=1/(b 1 - a 1)(b 2 - a 2).
Такое распределение называется равномерным в области D.
Найдем частные плотности распределения случайных величин x 1 и x 2
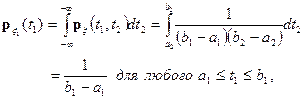
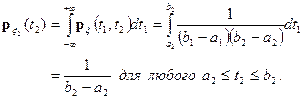
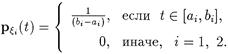 |
Мы получили, что случайные величины x 1 и x 2 имеют равномерные распределения с плотностями
 2014-02-02
2014-02-02 1746
1746