2014-02-02
778
Рассмотрим как выполняются сформулированные рекомендации при синтезе ФНЧ.
Очевидно, что для ФНЧ с частотой среза ωс жалеемая идеализированная характеристика Кр(ω) имеет вид:
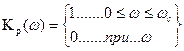Кр(ω)
1
Ω
Такая характеристика физически не реализуема, так как соответствующая ей К(ω) не отвечает критерием Пейли-Винера. Поэтому возникает задача подбора допустимой аппроксимируемой функции, которая может решаться разными способами. Один из способов ее решения основан на представлении характеристики Kp(ω) монотонной функцией вида:
, (*)
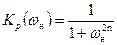где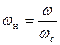 
- безмерная нормированная частота.
ФНЧ имеющий такие частотные свойства называется фильтром с максимально плоской характеристикой или фильтром Баттерворта. Целое число n=1,2,3… является периодом фильтра. Можно показать, что при любом n такой фильтр физически реализуем. Чем больше n, тем точнее аппроксимируется форма частотной характеристики.
Порядок фильтра подбирают обычно исходя из требований, предъявляемых к ослаблению сигналов с частотами w>1. Следующим этапом синтеза является определение полюсов передаточной функции K(Р), соответствующей выбранной форме (*)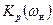 
. С этой целью, прежде всего, осуществляется переход от 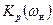к Kp(Р), выполняемый в соответствии с правилом:
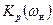= Kp(Р)
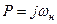, т.е. путем осуществления в (*) подстановки 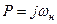. При этом имеем 
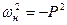или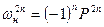 
, поэтому с учетом (*) получаем:
(**)
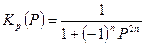Функция Kp(P) имеет 2n полюсов, являющихся решениями уравнения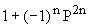 
. Можно показать, что все эти полюса определяются следующим выражением:
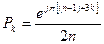где k=1,2,3...
Все эти полюсы расположены на окружности единичного радиуса на одинаковом угловом расстоянии друг от друга равном π/n.
Аргумент первого полюса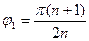 
последующего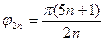 
На рисунке показано расположение полюсов n=1 и n=2,
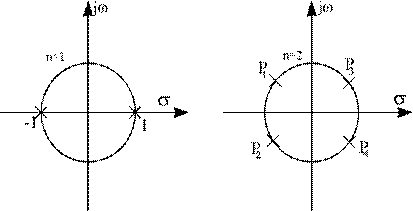
Определив все полюсы KР(Р) следует отобрать лишь те из них, которые расположились в левой полуплоскости, так как только в этом случае выполняется условие устойчивости фильтра, и считать их полюсами передаточной функции K(Р) синтезируемого фильтра. При этом выражение передаточной функции K(Р), например, для n=2 будет таким:
(***)
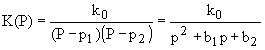Если n=3, то в знаменателе было бы три сомножителя, что соответствует полиному третьего порядка. Коэффициенты полиномов в знаменателе b1 и b2 и значение k0 обычно приводится в специальных таблицах пособиях по расчету фильтров. Для удовлетворительной аппроксимации идеальные характеристики ФНЧ с помощью функций Баттерворта требуют относительно высоких значений n. Для улучшенной аппроксимации этой характеристики часто применяется аппроксимация по Чебышеву, при которой Kp(wн) ФНЧ определяется следующей формулой:
(****)
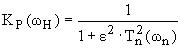где ε≤1 – постоянное число, называемое коэффициентом неравномерности АЧХ в полосе пропускания, а Tn(ωн) - полином Чебышева n-го порядка, определяемый выражением: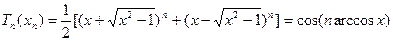
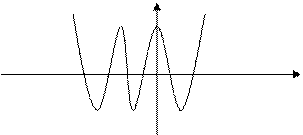
Полиномы Чебышева обладают следующими свойствами:
на интервале -1<х<1 они пульсируют вокруг нуля с амплитудой равной 1;
Тn(к)
-1 1 х
С помощью таких функций можно удачно аппроксимировать АЧХ ФНЧ. Из (****) видно, что в пределах полосы пропускания 0<ωн<1 величина Kp(ωн) будет изменяться в пределах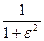 
. Если же ωн>1, то фильтр обеспечивает большое затухание сигнала.
Фильтры Чебышева являются оптимальными в том смысле, что не существует какого-либо другого фильтра n-го порядка, содержащего такие полюсы, который имел бы такие же или лучшие характеристики и в полосе пропускания, и в полосе непропускания.
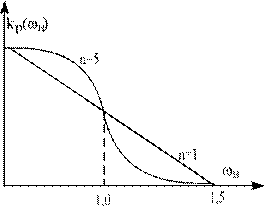
Графики зависимости Kp(ωн) приведены на рисунке: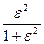 
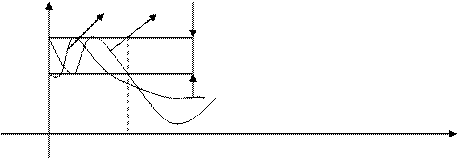Кр(ωн) n=1 n=3
1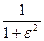
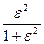
ωн=1 ωн
Из графиков видно, что частотные характеристики фильтров Чебышева не монотонны. Существуют и другие способы аппроксимации идеальных фильтров ФНИ, обладающие другими достоинствами. Например, эллиптические фильтры характеризуются тем, что их 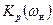имеет равновеликие пульсации и в полосе пропускания и в полосе непропускания. Эти фильтры являются оптимальными с точки зрения минимальной ширины переходной полосы, т.е. для заданных порядков фильтра и уровня пульсации обеспечивается наиболее быстрые переход от полосы пропускания к полосе непропускания. Однако передаточные функции таких фильтров кроме полюсов имеет и нули, что усложняет их реализацию.
Последний этап синтеза фильтра состоит в построении принципиальной схемы устройства и определения полиномов, входящих в схему устройства. Передаточную функцию К(Р) целесообразно представлять в виде произведения множителей, каждый из которых может являться передаточной функцией простейшего четырехполюсника. При этом комплексная характеристика такой цепи: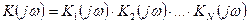 
, что соответствует последовательному включению звеньев с КЧХ 
,
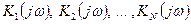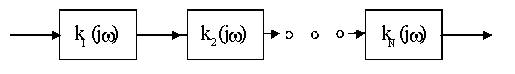
К(jω)
КЧХ 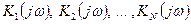должны быть такими, чтобы они реализовали те полюсы функции К(Р), которые были определены на этапе аппроксимации. Для создания фильтров требуются звенья двух видов. Звено первого порядка с единственным вещественным полюсом и звено второго порядка, имеющее пару комплексно сопряженных полюсов. Простейшим звеном первого порядка является, например, Г-образный четырехполюсник, для которого передаточная функция по напряжению 
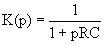. Здесь 
.
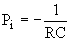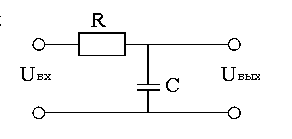
Звено второго порядка, имеющее два комплексно-сопряженных полюса также можно реализовать с помощью Г-образного четырехполюсника
,
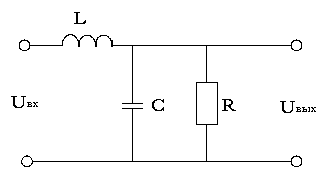
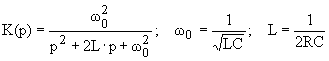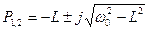
Приведенные здесь примеры реализации звеньев первого и второго порядка относятся к классу пассивных фильтров, характеризующихся тем, что их схемы не содержат усилительных элементов и состоят из набора определенным образом соединенных резисторов, конденсаторов и катушек индуктивности. Наличие последних обязательно для того, чтобы обеспечить возможность реализации передаточных функций с полюсами, лежащими не на осях координат комплексной плоскости, а в ее произвольных точках. Катушки индуктивности имеют большую массу, их трудно реализовать в интегральном исполнении. При их использовании появляются специфические погрешности. Все это обуславливает недостатки пассивных фильтров и ограничивает их применение. Независимыми они являются лишь там, где имеют место большие токи и напряжения. Наибольшее распространение получили активные фильтры, построенные на основе RC элементов и ОУ. При их использовании можно реализовать любые передаточные функции без катушек индуктивностей.
